Математик из МФТИ разработал новую усовершенствованную модель для описания динамики современных вооруженных конфликтов, которая впервые учитывает нелинейную зависимость передвижения войск от их собственной концентрации и плотности сил противника. Модель, основанная на системе нелинейных дифференциальных уравнений в частных производных, расширяет классические законы Ланчестера, добавляя в них пространственное измерение и реалистичные тактические факторы. Для решения этих сложных уравнений был создан устойчивый и точный численный метод, позволяющий моделировать возникновение и эволюцию «горячих точек» на поле боя. Результаты исследования, опубликованные в Journal of Applied Mathematics and Physics, открывают новые возможности для стратегического планирования и оптимизации военных операций.
С тех пор как в начале XX века английский инженер Фредерик Ланчестер вывел свои знаменитые уравнения, описывающие потери в бою, математика стала неотъемлемым инструментом военного анализа. Его простые формулы, связывающие численность сторон и их боевую эффективность, легли в основу теории исследования операций. Однако классические модели Ланчестера обладают существенным недостатком: они рассматривают армии как однородные массы, не учитывая их расположение и передвижение в пространстве. В современных конфликтах, где мобильность, концентрация сил на ключевых направлениях и избегание окружения играют решающую роль, такой подход недостаточен. Поле боя — это не шахматная доска со статичными фигурами, а динамичная среда, где плотность войск постоянно меняется, влияя на их способность маневрировать и вести огонь.
Чтобы преодолеть эти ограничения, Никита Борисов из Физтех-школы прикладной математики и информатики МФТИ предложил новый подход. Он представил поле боя как двумерное пространство, в каждой точке которого плотность сил двух противоборствующих сторон описывается системой уравнений реакции-диффузии. В этой системе, помимо классических членов, описывающих потери в бою (реакция), присутствуют и диффузионные члены, отвечающие за передвижение войск. Ключевое нововведение состоит в том, что коэффициент диффузии, то есть «подвижность» войск, не является постоянной величиной. Он нелинейно зависит от концентрации как своих, так и вражеских сил. Такой подход позволяет моделировать реалистичные тактические сценарии: например, высокая концентрация своих сил может облегчать логистику и увеличивать мобильность («эффект блицкрига»), в то время как присутствие противника, наоборот, сковывает передвижение («эффект сковывания»).
Для решения получившейся сложной системы нелинейных уравнений ученый применил высокоэффективный численный метод, известный как метод переменных направлений (ADI). Этот метод отличается высокой устойчивостью и точностью, позволяя проводить надежные симуляции даже для сильно нелинейных сценариев. Прежде чем приступить к моделированию, автор тщательно проверил корректность своего численного алгоритма, сравнив его результаты с известными аналитическими решениями для более простых случаев, таких как бегущие волны и режимы взрывного роста (blow-up), подтвердив высокую точность и надежность своего подхода.
Результаты численного моделирования продемонстрировали богатую и сложную динамику, недоступную классическим моделям. В ходе симуляций на виртуальном поле боя самопроизвольно формировались и эволюционировали сложные пространственные структуры. Модель показала, как из начального равномерного распределения сил одна из сторон со временем концентрируется в виде компактного, локализованного «ударного кулака», в то время как силы противника оказываются более рассредоточенными.
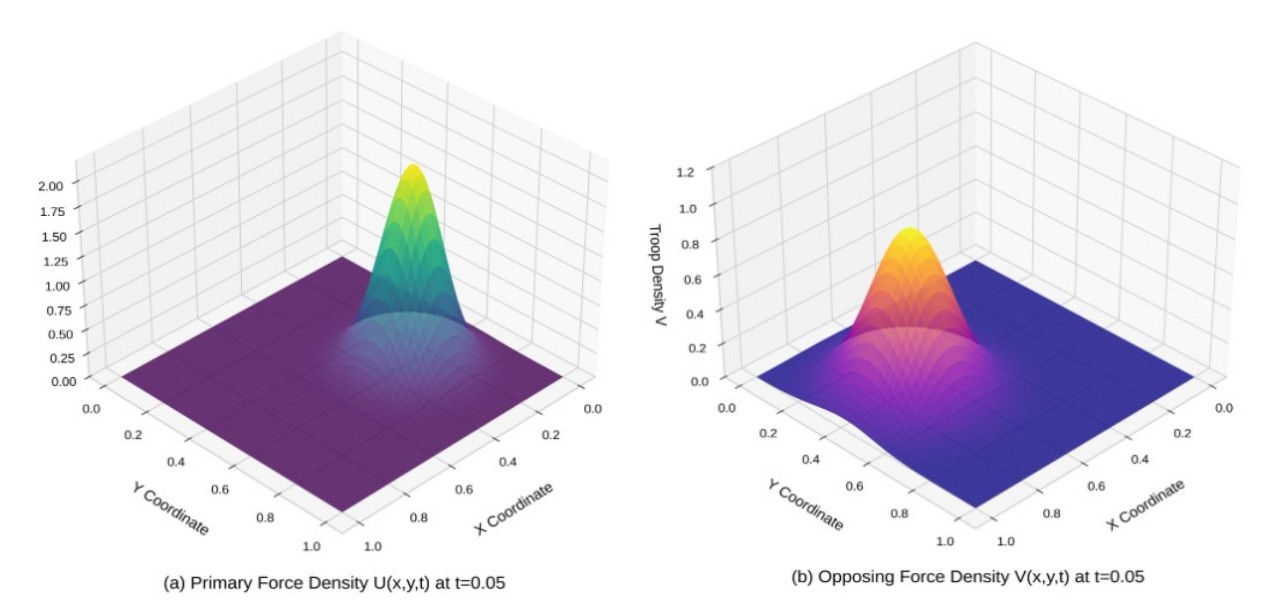
Рисунок 1. Пространственное распределение сил на поле боя, смоделированное с помощью новых уравнений. Верхний график (а) показывает, как атакующая группа (Primary Force) концентрируется в виде мощного локализованного «ударного кулака». Нижний график (b) демонстрирует, что силы противника (Opposing Force) в тот же момент времени имеют более рассредоточенную и слабую конфигурацию. Модель наглядно показывает самоорганизацию войск и формирование «горячих точек» в ходе боя. Источник: Journal of Applied Mathematics and Physics.
Эти визуализации, представленные в статье в виде трехмерных графиков плотности, наглядно демонстрируют способность модели предсказывать возникновение критических зон концентрации войск, которые могут стать решающими для исхода сражения.
«Меня как ученого интересовала проблема создания математического инструмента, который говорит на языке тактики,— рассказал Никита Борисов, аспирант кафедры анализа систем и решений МФТИ.— Вместо абстрактных чисел модель оперирует понятиями концентрации сил, мобильности, логистической поддержки и зон воспрещения доступа. Наша модель показывает, как эти факторы взаимодействуют в пространстве и времени, приводя к самоорганизации на поле боя — формированию фронтов, направленных ударов, прорывов и окружений. Это шаг от простой «бухгалтерии потерь» к полноценному динамическому моделированию боевых действий».
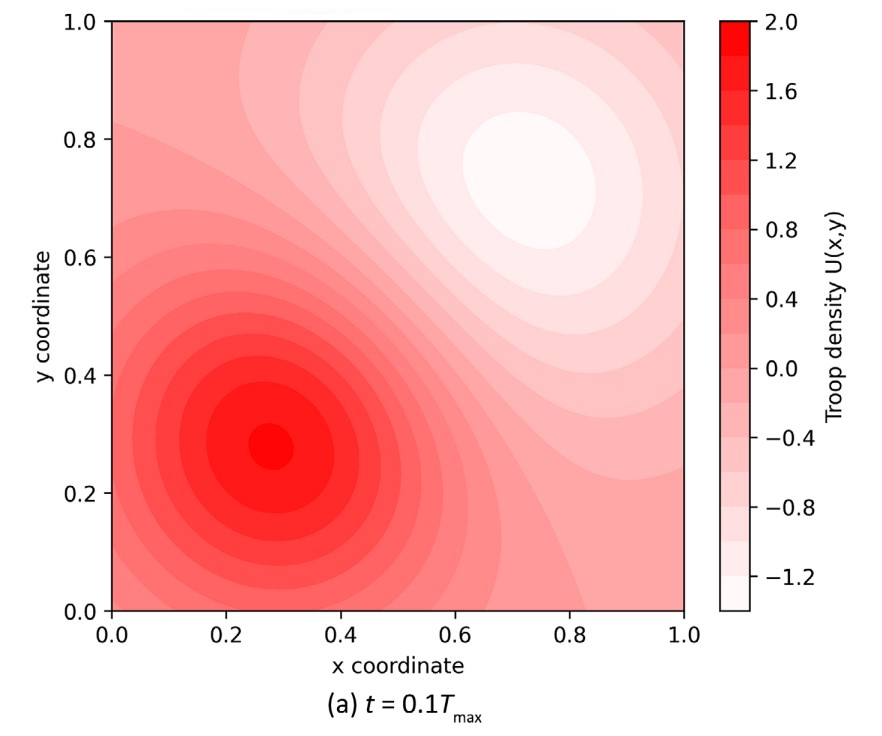
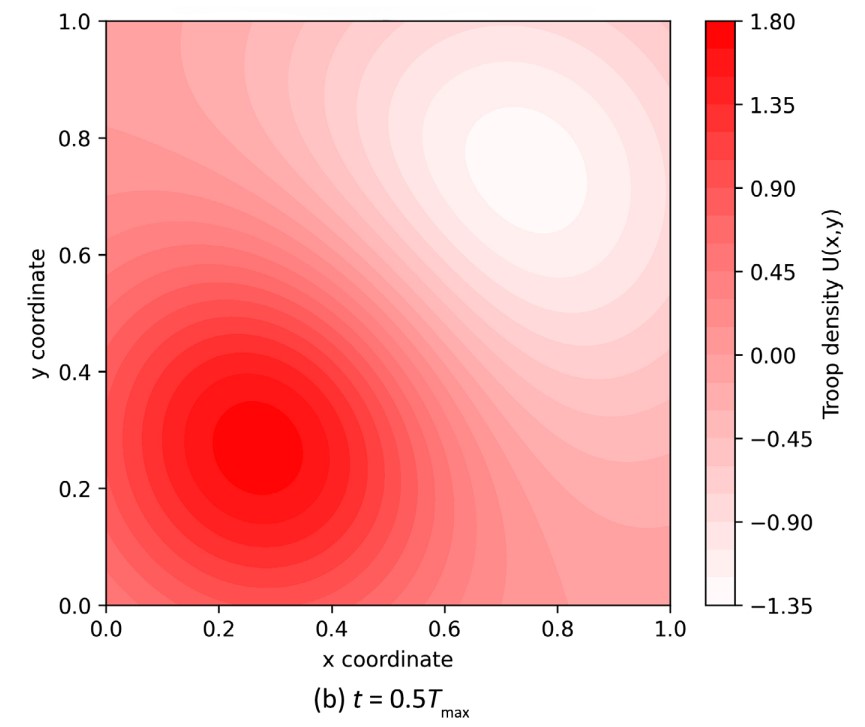
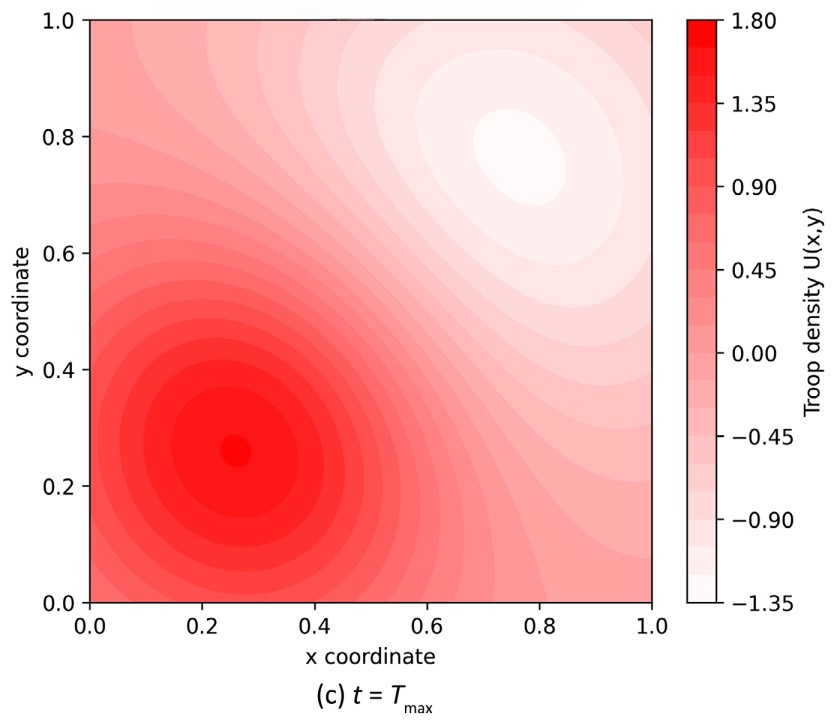
Рисунок 2. Эволюция плотности атакующих сил во времени. На начальном этапе (a) войска сконцентрированы в центре. В середине боя (b) они начинают продвигаться и расширять зону контроля. К концу симуляции (c) формируется устойчивый фронт, прижатый к границам «вражеской» территории. Эти тепловые карты показывают динамику боя. Источник: Journal of Applied Mathematics and Physics.
Предложенная модель обладает большой гибкостью. Варьируя параметры в нелинейных коэффициентах диффузии, можно моделировать различные тактические сценарии. Например, можно симулировать «блицкриг», где мобильность резко возрастает с концентрацией сил; «активную оборону», где присутствие противника сильно замедляет продвижение; или даже «партизанскую войну», где высокая плотность войск приводит к их рассредоточению. Кроме того, модель выявила существование характерного пространственного масштаба, определяемого соотношением мобильности сил и интенсивности их огневого воздействия. Этот масштаб, по оценкам автора, составляет около 1.4 км и может интерпретироваться как оптимальное расстояние между подразделениями для обеспечения взаимной поддержки.
Результаты исследования могут быть применены для математического моделирования в военной стратегии и тактике. Разработанный инструмент может быть использован для анализа различных сценариев, оптимизации распределения сил, оценки эффективности новых видов вооружения и планирования логистики. В будущем автор планирует усовершенствовать модель, добавив в нее трехмерное пространство (например, для учета авиации и рельефа местности), адаптивные шаги по времени, что еще больше повысит ее реалистичность и прогностическую силу, а также стохастические члены, которые позволят сделать моделирование еще более точным (например, противник стреляет и может не попасть).
Научная статья: Borisov, N.D. (2025) Development of Lanchester-Type Spatial Models with Obtaining Localized Solutions for the Interaction of Two Groups. Journal of Applied Mathematics and Physics, 13, 2332-2342. https://doi.org/10.4236/jamp.2025.137132

