
Масаки Касивара
Фото: Peter Badge/Typos1/The Abel Prize
В марте был объявлен новый лауреат Абелевской премии (её еще называют «Нобелевской премией по математике») — им стал японец Масаки Касивара. О том, чем именно он известен, мы попросили рассказать Михаила Цфасмана, вице-президента Независимого московского университета и научного руководителя Высшей школы современной математики МФТИ.
Касивару я привык называть «Кашиварой» потому что мы, естественно, читали его статьи по-английски, а он там пишется через «sh» (Masaki Kashiwara). Он старше меня лет на семь, а его наиболее значимые работы появились, когда я ещё был студентом мехмата. Ну, какие-то появились и до, но его имя я впервые услышал, году, наверное, в 1973-74-м. Для меня эти работы очень тесно связаны с работами другого Абелевского лауреата, Пьера Делиня, а также с работами людей, которых я очень хорошо знаю лично: Иосифа Бернштейна и Александра Бейлинсона.
Касивара мне больше всего известен тем, что он один из авторов концепции D-модуля. Что такое D-модуль? В сознании многих людей существует две совершенно далекие друг от друга области математики. Первая — это дифференциальные уравнения в частных производных. Это вещь, которая очень нам нужна для физики, для разных других наук, ну и с точки зрения самой математики тоже очень интересная. Мы привыкли, что это часть науки о непрерывных функциях, о производных и других таких вещах — в широком смысле, математического анализа. Того, чему нас начинают учить на первом курсе университета и даже немножко в старших классах математических школ. И совершенно отдельно от этого в массовом сознании стоят алгебра и геометрия, из которых родилась алгебраическая геометрия, которую я очень люблю и с которой, собственно, связано моё базовое математическое образование.
А смысл D-модулей в том, чтобы две упомянутых области объединить — научиться решать задачи, связанные с дифференциальными уравнениями в частных производных в терминах и техниках, которые более свойственны алгебраической геометрии. Как это достигается? Дальше я буду сознательно огрублять, чтобы было понятнее — поэтому если среди аудитории есть математики, то пусть они ко мне не сильно придираются.
Одним из основных инструментов и объектов математики являются многочлены. Что такое многочлен, мы знаем ещё по школе. Это сумма каких-то коэффициентов, умноженных на произведения неизвестных. То есть сумма мономов.
Из математического анализа мы знаем, что есть такой оператор, как дифференциал. И если переменных много, то мы можем дифференцировать по одной переменной, по другой переменной, и так далее. А если символы этих дифференциалов мы будем — чисто формально — считать другими переменными, то есть у нас появляются многочлены не только от переменных, но и от дифференцирования по этим переменным. И с этим математическим объектом можно работать. После этого оказывается, что — в очень грубом смысле — дифференциальное уравнение является некоторой структурой, которая называется модулем над кольцом дифференциальных операторов. То есть чем-то, на чём действуют вот эти многочлены.
Это исходное понятие D-модуля. Когда Касивара их придумывал, то он очень сильно опирался на работы своего учителя Микио Сато (основатель алгебраического анализа — прим. «ЗН»), и на работы Иосифа Бернштейна, которые были перед этим. Бернштейн, грубо говоря, его ровесник. Но для меня самым замечательным является не это.
Самым замечательным для меня является вот что. Что такое алгебраическая геометрия? Нас в школе учили, что окружность радиусом единица с центром в нуле можно задать уравнением x2 + y2 = 1. И вот всё то, что можно задать системой уравнений, — где каждое из этих уравнений это многочлен, который равен нулю, — от нескольких переменных, это то, называется алгебраическим многообразием.
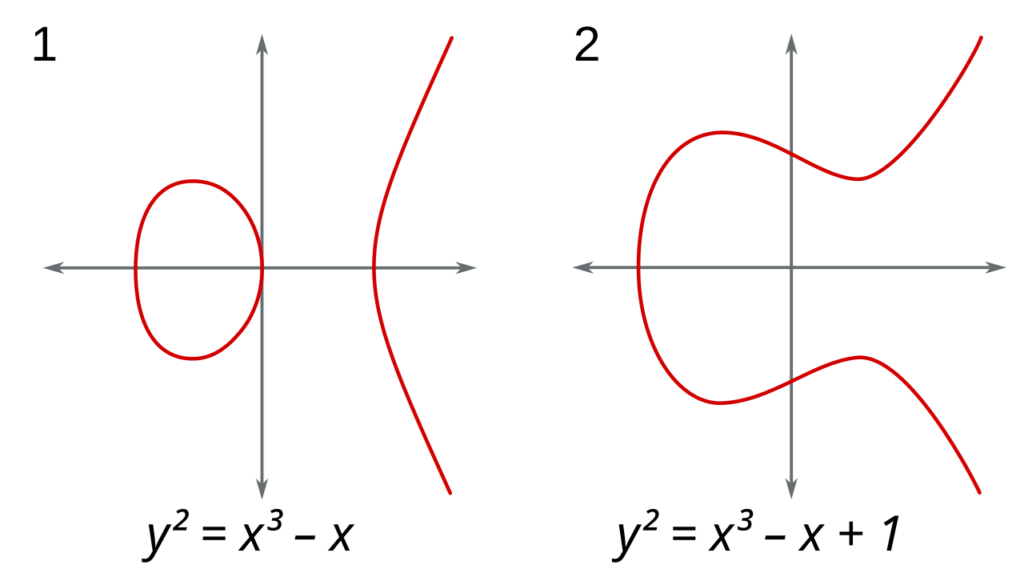
Графики эллиптических кривых над полем вещественных чисел — пример алгебраического многообразия
Изучение этих алгебраических многообразий может производиться как геометрическими методами — например, какую-нибудь касательную провести, или что-нибудь ещё, — так и алгебраическими. То есть можно рассматривать какие-то функции на этих кривых поверхностях, которые тоже задаются многочленами, и здесь возникает вот такая наука. В этой науке неким прорывом стало применение методов, которые родились в другой области математики, алгебраической топологии. Тогда возникли такие понятия, как понятие групп гомологий, групп когомологий, а потом и несколько более общее понятие — пучок.
Что такое пучок, я объяснять не буду, потому что нематематику я это не объясню. Но, опять же, это некая надстройка над алгебраическим многообразием. И вот эти D-модули, которые открыл Касивара, они очень похожи на эти пучки, хотя и не совсем. И вот в начале 80-х годов Пьер Делинь, Бернштейн и Александр Бейлинсон сделали замечательную работу, в которой появилось понятие извращённого пучка. Иногда его ещё называют перверсным. По-английски perverse sheaf, самый первый термин был французский — faisceaux pervers. Что в нём такого извращённого? То, что извращённый пучок пучком не является. Он является их комбинацией, комплексом пучков. И вот оказалось, что D-модули связаны с этой наукой. Это очень хорошо с тех пор развивалось, как самим Каcиварой, так и массой народа по всему миру, и сегодня применяется в очень разных областях математики.
Это лишь одно из его больших достижений. Другое достижение — это то, что называется микролокальный анализ. Есть у вас функция. Вы на эту функцию можете смотреть целиком. Для простоты, представьте себе просто какой-нибудь многочлен от одной переменной над вещественными числами. И вы на неё можете смотреть глобально, —скажем, как на весь график сразу, — а можете взять и посмотреть, что происходит рядом с точкой. Понятие производной, например, это локальное понятие, потому что оно относится не ко всему графику, а ровно к той точке, в которой вы проводите касательную. А дальше вам уже надо представлять не кривую, а хотя бы поверхность. Представьте поверхность, точку на ней и касательную плоскость в этой точке. И после этого давайте смотреть не только на маленькую-маленькую окрестность этой точки, но и возьмём в этой касательной плоскости какую-нибудь касательную прямую и посмотрим на окрестность этой касательной прямой. Когда мы смотрим и на то, и на другое, то это уже называется не локальный анализ, а микролокальный анализ. Здесь я опять же сильно огрубил, потому что надо брать не касательное пространство, а касательное расслоение, но мы в такие детали углубляться не будем. Важно тут то, что мы изучаем еще более локально, чем просто в точке. Вот эта штука тоже оказалась очень полезна для дифференциальных уравнений, и у Касивары есть красивые работы на эту тему.
Ну, и многое-многое другое. Он работал с обобщенными функциями. Обобщенные функции — это такая тоже замечательная наука, существует многотомник Израиля Гельфанда, который так и называется, «Обобщенные функции». И даже я, занимаясь в основном теорией чисел и алгебраической геометрией, в своих работах эти обобщенные функции использую, они теперь вообще везде. Он занимался этим и другими похожими на это вещами.
Что еще можно сказать? Касивара являет собой редкий случай японского математика очень высокого уровня, который в основном работал в Японии, потому что всякие знаменитые японские математики, как Кодайра и Мори, лауреаты Филдсовских премий, — они значимую часть своей жизни провели все-таки в Америке. Почему Касивара так решил, я не знаю, я с ним лично не знаком. Но его карьера складывалась, в общем, довольно удачным образом. После Токийского университета, где он сделал своих D-модули (они появились уже в его магистерском дипломе), он учился в аспирантуре в Киото, и там же, в Киото, и остался. В Киото есть пара научно-исследовательских институтов, в одном из них я когда-то провёл месяц — там множество иностранцев и очень стимулирующая атмосфера. Да и кроме того, Япония, все-таки, одна из основных математических держав. И поэтому остаться в Японии — это не остаться в одиночестве.
По-моему, год или два Касивара провёл Принстоне, довольно много ездил во Францию, потому что был там живёт замечательный специалист по микролокальному анализу, Пьер Шапира. И у него с ним есть работы (в первую очередь, «Пучки на многообразиях» — прим. «ЗН») , и с Бернаром Мальгранжем.
Еще можно сказать, что D-модули применяются в физике. Правда, в такой, которую многие физики физикой не считают — в теории струн. Мы привыкли к тому, что наше пространство, сколько бы у него, по нашему мнению, не было измерений, — что оно гладкое. В том смысле, что там нет шипов, нет самопересечений и прочих вещей, которые мы называем особенностями (или сингулярностями). А многообразия Калаби — Яу, связанные с теми или иными физическими задачами, бывают особыми в этом смысле. И, грубо говоря, решать дифференциальные уравнения на этих многообразиях становится намного труднее. А можно сказать, что изучать их геометрию становится много труднее.

Двумерные проекции пятимерного (слева) и трехмерного (справа) пространств Калаби — Яу
Калаби — Яу это конечномерное многообразие, но если там поверхность с особенностью, то там уже не одна касательная плоскость, их много. И возникают всякие проблемы. Тут как раз на помощь приходят D-модули, особенно извращенные пучки. Это одна вещь. Вторая вещь заключается в том, что всё это тесно связано с теорией представлений групп, которой у нас занимался уже упоминавшийся Израиль Моисеевич Гельфанд и очень много других людей.
И сейчас есть такая очень модная область, называется программа Ленглендса. Её основатель, Роберт Ленглендс, за нее получил Абелевскую премию в 2018 году. И вот есть арифметическая теория Ленглендса, и есть геометрическая. Геометрическую сейчас развивают в Чикагском университете как раз Бейлинсон и другой наш филдсовский лауреат, Владимир Дринфельд. Они этим много занимаются. И там у них тоже необходимы эти извращенные пучки.
В заключение я бы сказал так — если бы меня спросили, кому надо давать Абелевскую премию, то имя Касивары пришло бы мне на ум не первым. Отчасти это связано с тем, что, все-таки, эта область не совсем моя. Но при этом его имя вполне на слуху. Но! Что с Филдсовской медалью, что с Абелевской премией — иногда бывает, что достойный человек их не получает. Но я почти не знаю или вовсе не знаю ситуаций, когда их получил кто-то недостойный. А Масаки Касивара — замечательный математик. И за это ему и дали премию Абеля.
1

