Исследователи из МФТИ впервые систематически изучили, как изменяется и стабилизируется процесс обучения нейронных сетей по мере добавления новых данных. Их работа, сочетающая теоретический анализ и обширные эксперименты, показывает, что так называемый «ландшафт функции потерь» нейросети сходится к определенной форме при увеличении размера выборки, что имеет важные последствия для понимания глубинного обучения и разработки методов определения необходимого объема данных. Исследование опубликовано в Doklady Mathematics.
Нейронные сети – мощный инструмент современного искусственного интеллекта, лежащий в основе множества технологий, от распознавания лиц на смартфонах до беспилотных автомобилей и медицинских диагнозов. Эти сложные математические модели, вдохновленные строением человеческого мозга, обучаются на огромных массивах данных. Процесс обучения, по сути, является поиском оптимальных настроек параметров нейронной сети, которые минимизируют ошибки предсказаний.
Ключевым понятием здесь является функция потерь. Это математическая мера того, насколько «неправильно» работает нейросеть на данном этапе обучения. Чем ниже значение функции потерь, тем лучше сеть справляется с задачей. Эту функцию можно изобразить подобно тому, как изображают карту местности с горами и долинами. Каждая точка на этой карте соответствует определенному набору параметров нейросети, а высота в этой точке – значению функции потерь. Такая многомерная «карта» называется ландшафтом функции потерь.
Обучение нейросети – это как спуск с горы в самую глубокую долину на этой карте. Однако ландшафт потерь современных нейросетей чрезвычайно сложен, с бесчисленным количеством «локальных минимумов» (небольших долин) и потенциально одним или несколькими «глобальными минимумами» (самыми глубокими точками). Найти хороший минимум – непростая задача.
Ученые давно изучают геометрию этого ландшафта. Например, известно, что более «плоские», широкие долины часто соответствуют моделям, которые лучше обобщают – то есть хорошо работают не только на обучающих данных, но и на новых, ранее не виданных примерах. Для анализа формы ландшафта, особенно кривизны вокруг минимумов, используется математический инструмент – матрица Гессе, содержащая вторые производные функции потерь. Анализ спектра Гессиана (набора его собственных значений) выявил характерные особенности: большинство значений близки к нулю, но есть и несколько больших значений, указывающих на направления резкого изменения потерь.
Однако, несмотря на значительный прогресс в понимании «статичной» геометрии ландшафта для заданного набора данных, оставался открытым фундаментальный вопрос: как этот ландшафт изменяется, когда мы добавляем в обучающую выборку новые данные? Становится ли он стабильнее? Сходится ли к какой-то определенной форме? Именно эту «белую зону» и взялись исследовать авторы новой работы.
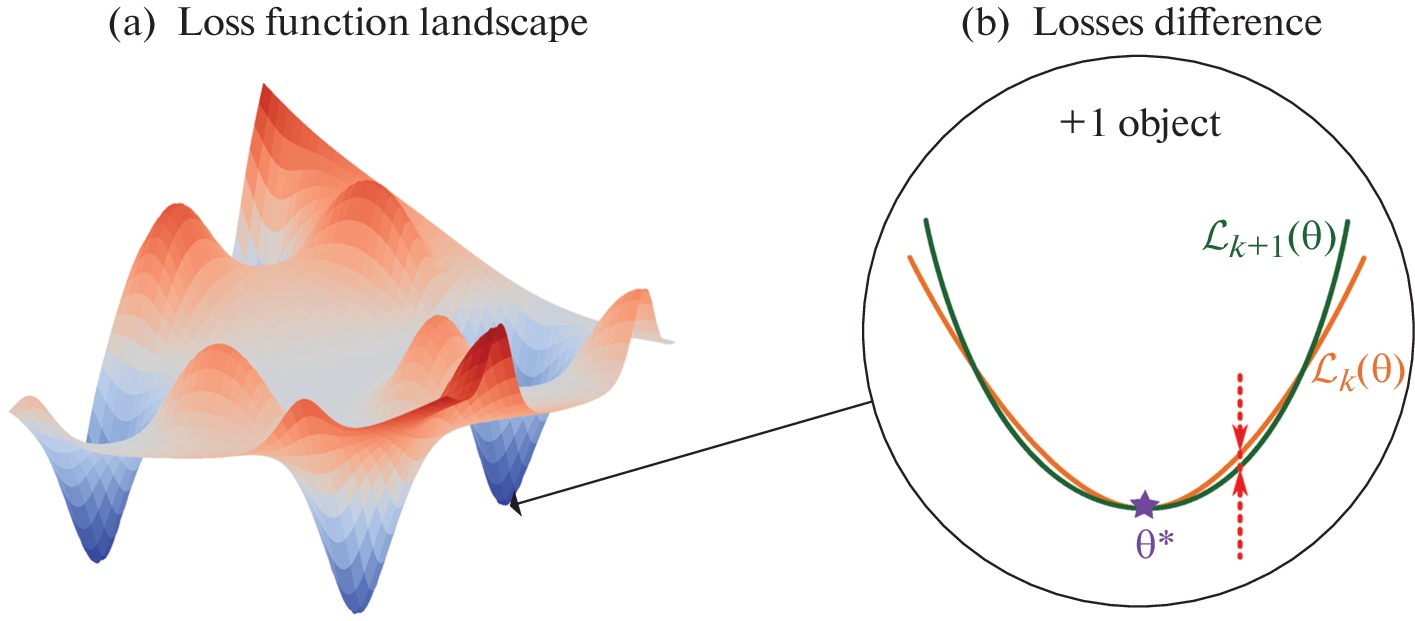
Рисунок 1. (a) ландшафт функции потерь, который является поверхностью в пространстве параметров. (b) разница потерь, которая возникает, когда к набору данных добавляется еще один объект. Источник: Doklady Mathematics.
Исследователи из МФТИ поставили перед собой четкую цель: понять и количественно описать, как меняется ландшафт функции потерь – в частности, значение самой функции потерь в окрестности найденного минимума – при добавлении в обучающую выборку всего одного нового объекта. Их интересовало, будет ли эта разница уменьшаться с ростом общего числа объектов, и если да, то с какой скоростью. Они сначала обучали сеть на всем доступном наборе данных, чтобы найти точку минимума (или близкую к нему). Затем они брали подмножества данных разного размера (от малого до большого), добавляли по одному объекту и измеряли, насколько в среднем изменяется значение функции потерь в найденной точке минимума. Этот процесс повторялся многократно для усреднения результатов. Эксперименты проводились как с использованием «сырых» пикселей изображений в качестве входа, так и с использованием признаков, предварительно извлеченных из изображений с помощью мощной предобученной модели.
И теоретический анализ, и экспериментальные данные привели к одному и тому же выводу: ландшафт функции потерь действительно стабилизируется (почти перестает меняться) по мере увеличения размера выборки. Теоретический анализ показал, что разница между средним значением потерь для выборки из k+1 объекта и выборки из k объектов (в окрестности минимума) стремится к нулю, когда k стремится к бесконечности. При этом полученная верхняя граница для этой разницы убывает примерно как 1/k (сублинейная скорость сходимости). Теоретические оценки также предсказали, как на эту сходимость влияют параметры сети: увеличение числа слоев L может замедлить сходимость (экспоненциальная зависимость в оценке), в то время как влияние ширины слоев h оказалось более сложным (степенная зависимость, но с множителем, зависящим от величины весов сети).
Эксперименты подтвердили результаты теоретического анализа на всех использованных наборах данных и для разных архитектур. Во всех экспериментах наблюдалось четкое уменьшение разницы значений функции потерь при увеличении размера выборки, что подтверждает теоретический вывод о сходимости. Влияние архитектуры также качественно совпало с теорией: добавление слоев действительно несколько увеличивало измеряемую разницу (замедляло сходимость), а увеличение ширины слоев, вопреки интуиции и грубой теоретической оценке, уменьшало разницу.
Исследователи объясняют это тем, что для относительно простых задач классификации изображений более широкие сети достигают лучших (более низких) значений потерь, и их ландшафт быстрее стабилизируется, а также тем, что константы, ограничивающие веса сети на практике, могут быть малы. Важно, что сходимость наблюдалась независимо от того, подавались ли на вход сети сырые пиксели или предобработанные признаки.
«Мы привыкли думать о ландшафте потерь как о статичной карте для конкретного набора данных, – рассказал Андрей Грабовой, доцент кафедры интеллектуальных систем МФТИ – Наша работа показывает его динамическую природу: как он ‘устаканивается’ и перестает существенно меняться по мере того, как сеть ‘видит’ все больше и больше примеров. Это предсказуемое поведение открывает двери к пониманию того, когда дальнейшее увеличение данных уже не приносит кардинальных изменений в локально выученную модель, что критически важно для эффективного обучения».
Никита Киселев, студент 5-го курса МФТИ, добавил: «Главный результат нашего исследования в том, что мы впервые систематически исследовали вопрос о влиянии размера выборки на геометрию ландшафта потерь. Предыдущие исследования фокусировались либо на статичной геометрии для фиксированного датасета, либо на динамике обучения во времени (по итерациям оптимизации), но не на том, как сам ландшафт эволюционирует с количеством данных. Мы не только поставили этот вопрос, но и предоставили теоретический анализ сходимости, осуществив вывод математических оценок скорости стабилизации ландшафта, показали, как количество слоев нейронной сети и их ширина влияют на эту сходимость, а также проверили выводы на практике на реальных задачах»
Понимание того, что ландшафт потерь сходится, имеет значительные практические последствия. Самое очевидное из них заключается в том, что на основе этого можно разработать методы, которые отслеживают эту стабилизацию в процессе добавления данных и позволяют эффективно определять достаточный размер выборки. Как только ландшафт перестает существенно меняться, можно сделать вывод, что для данной архитектуры и задачи данных, вероятно, достаточно. Это позволит экономить огромные ресурсы на сбор, разметку и обработку избыточных данных, а также на вычислительные мощности для обучения.
Менее очевидные применения связаны с тем, что понимание того, как меняется ландшафт функции потерь, может помочь в разработке более оптимальных вычислительных архитектур и более эффективных адаптивных алгоритмов машинного обучения нейронных сетей.
Научная статья: Kiselev, N.S., Grabovoy, A.V. Unraveling the Hessian: A Key to Smooth Convergence in Loss Function Landscapes. Dokl. Math. 110 (Suppl 1), S49–S61 (2024). https://doi.org/10.1134/S1064562424601987

