Коллектив ученых из МФТИ и МГУ провел важное исследование фундаментальных законов природы, значительно расширив возможности одного из самых перспективных инструментов для исследования М-теории – гипотетической «теории всего». Они обобщили математический метод, известный как три-векторные деформации, на полные, без каких-либо упрощений, уравнения 11-мерной супергравитации в рамках Исключительной Теории Поля. Результатом стали явные «рецепты» того, как можно систематически изменять (или «деформировать») геометрию и поля любого известного 11-мерного пространства-времени, чтобы получить новые, ранее неизвестные решения, подчиняющиеся тем же элегантным алгебраическим условиям, что и в более простых случаях. Эта работа, опубликованная в The European Physical Journal C, открывает новые перспективы в понимании структуры М-теории и ее связи с квантовой теорией поля через голографический принцип.
Исследование выполнено при поддержке гранта Российского научного фонда RSCF-20-72-10144.
Одной из величайших задач современной теоретической физики является построение единой теории, описывающей все фундаментальные силы и частицы природы, включая гравитацию, – так называемой «Теории Всего». Огромный толчок исследованиям в этой области дала гипотеза о калибровочно-гравитационном соответствии (AdS/CFT или голография). Этот принцип утверждает, что теория гравитации (например, теория струн или М-теория) в определенном искривленном пространстве-времени (типа анти-де Ситтера, AdS) математически эквивалентна («дуальна») квантовой теории поля , живущей на границе этого пространства. Это как если бы сложный трехмерный объект (гравитация) полностью описывался двумерной голограммой на его поверхности.
Один из успешных подходов – это метод деформаций. Идея состоит в том, чтобы взять хорошо изученное, высокосимметричное решение и систематически его «исказить» или «деформировать», чтобы получить новое решение с меньшей симметрией, но все еще поддающееся анализу. Работа Лунина и Малдасены показала, как такие деформации гравитационных решений связаны с добавлением определенных операторов в дуальную квантовую теорию поля.
Прорыв произошел с открытием обобщенного уравнения Янг-Бакстера (genCYBE) и более сложных поли-векторных деформаций (три-векторных, шести-векторных и т.д.).
Для последовательного описания этих сложных поли-векторных деформаций потребовался новый математический язык – исключительная теория поля (ExFT).
В предыдущих работах был разработан формализм три-векторных деформаций на основе SL(5) ExFT (которая соответствует действию U-дуальности в 4-мерном подпространстве 11-мерного пространства-времени). Однако этот формализм страдал от существенного недостатка: он требовал серьезных упрощений.
Авторы новой статьи поставили перед собой амбициозную цель: расширить формализм три-векторных деформаций так, чтобы он был применим к самым общим конфигурациям метрики, и вывести явные правила преобразования этих полей.
Исследователи начали с общего разложения полей 11-мерной супергравитации на компоненты, соответствующие разделению 11 измерений на 7 внешних и 4 внутренних (7+4), не предполагая, что какие-либо компоненты равны нулю. Они тщательно отобразили все эти компоненты, которые преобразуются линейно под действием группы SL(5). Этот шаг потребовал введения дополнительных («дуальных») полей для ковариантности формулировки исключительной теории поля. Далее они записали полные уравнения движения 11-мерной супергравитации в SL(5)-ковариантной форме, используя язык исключительной теории поля и так называемые «обобщенные потоки» – объекты, которые ведут себя как тензоры напряженности в этом формализме. И после этого, наконец, определили три-векторную деформацию как SL(5)-преобразование.
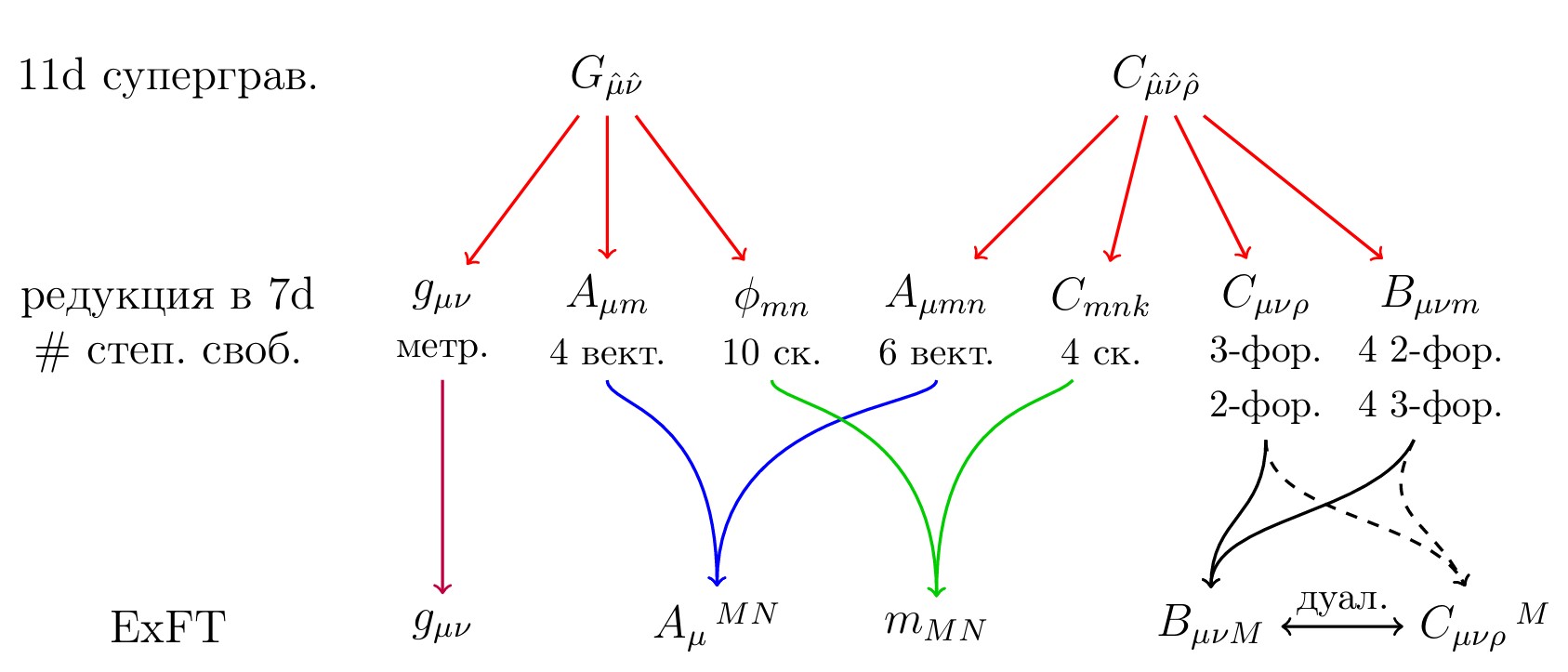
Рисунок 1. Редукция полей 11-мерной супергравитации в мультиплеты семи измерений и их объединение в SL(5) мультиплеты при помощи дуализации. Большие латинские индексы M,N,K,… обозначают фундаментальное представление 5 группы SL(5), маленькие латинские индексы m,n,k,… обозначают координаты на внутреннем пространстве T4 (фундаментальное представление 4 группы GL(4)). Источник: Мусаев.
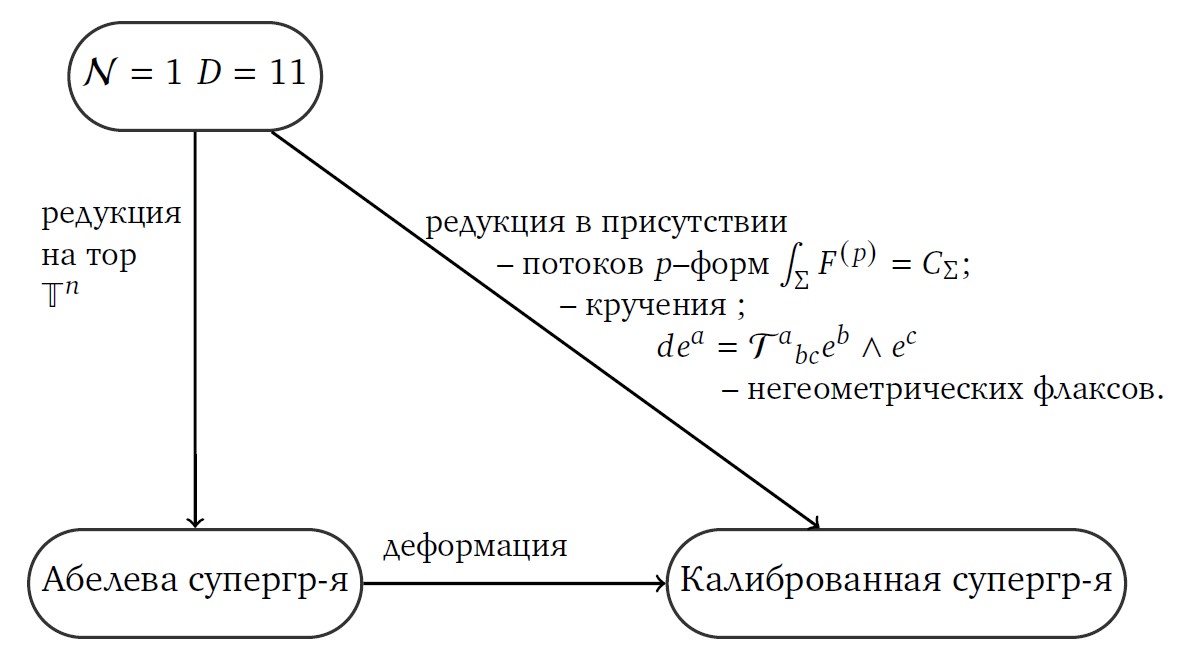
Рисунок 2. Диаграмма иллюстрирует отношения между торическими размерными редукциями N = 1 𝐷 = 11 супергравитации, суперсимметричными деформациями абелевой супергравитации в формализме тензора погружения и размерными редукциями с ненулевыми флаксами. Источник: Мусаев.
Ученым удалось проанализировать, как ковариантные уравнения движения исключительной теории поля изменяются под действием этой деформации. Они показали, что если параметры деформации удовлетворяют обобщенному уравнению Янг-Бакстера и, дополнительно, условию унимодулярности, а векторы Киллинга удовлетворяют естественным условиям совместимости с полями, то деформированные поля также будут удовлетворять исходным уравнениям движения.
Векторы Киллинга – это математические объекты, описывающие непрерывные симметрии пространства (например, возможность вращения или сдвига без изменения геометрии). Деформации, как бивекторные, так и поливекторные, строятся вдоль набора таких векторов.
Самое важное для практического применения – авторы сформулировали правила преобразования ковариантных полей исключительной теории поля в терминах компонент обычных 11-мерной метрики и 3-формы. Полученные таким образом явные и общие формулы показывают, как именно изменяются метрика и калибровочный потенциал (а также его напряженность) при три-векторной деформации.
Главный результат работы – создание универсального и явного формализма для три-векторных деформаций произвольных решений 11-мерной супергравитации в рамках SL(5) исключительной теории поля. При этим, SL(5) – это группа U-дуальности, действующая в 4-мерного подпространстве полного 11-мерного пространства-времени.
Данный результат превращает три-векторные деформации из инструмента, применимого к ограниченному классу решений, в мощный и универсальный метод исследования всего пространства решений 11-мерной супергравитации.
Эдвард Мусаев, доцент кафедры теоретической физики им. Л.Д. Ландау МФТИ, прокомментировал:«Работа напрямую решает проблему ограниченности предыдущих подходов. Новый метод позволяет систематически конструировать новые, сложные конфигурации пространства-времени и полей, что расширяет наше понимание возможного вида 11-мерных миров, описываемых М-теорией, и открывает возможность строить решения уравнений супергравитации, дуальные квантовым теориям поля с меньшей симметрией. При этом применение полученных результатов не ограничивается только областью квантовой гравитации: уравнение Янг-Бакстера связывает эту область с теорией интегрируемых систем и квантовыми группами, и дальнейшее изучение деформаций может выявить новые математические структуры, применимые как в квантовой теории поля, так и, например, для решения задач физики твердого тела».
Научная статья: Sergei Barakin, Kirill Gubarev, Edvard T. Musaev. Generalized 11D supergravity equations from tri-vector deformations. The European Physical Journal C, Volume 84, article number 1312 (23 December 2024). https://doi.org/10.1140/epjc/s10052-024-13688-4

