
Все электронные устройства, которыми мы пользуемся сегодня — от серверных ферм до смартфонов,— относятся к классическим вычислителям. Их принципиальное устройство впервые было описано Джоном фон Нейманом в 1945 году. Вычислитель «фон-Неймановской» архитектуры воплощает модель Тьюринга—Чёрча (она же «машина Тьюринга»), формализовавшую понятие алгоритма. Этим массив вычислителей, однако, не ограничивается.
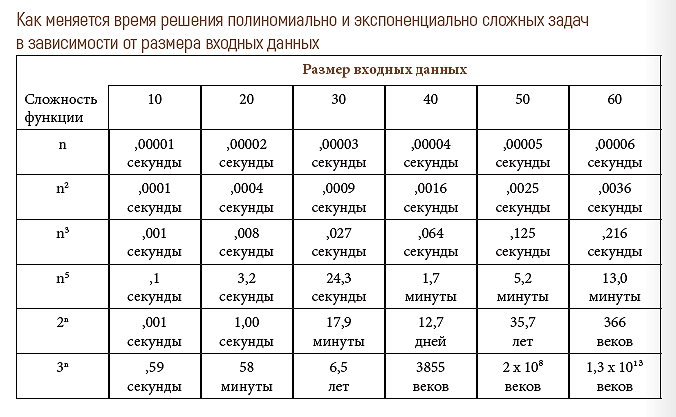
Основные элементы классической машины — «логика», память и каналы передачи данных. Процессор выполняет простейшие логические операции, сложение и сравнение чисел. Эти операции оперируют битами, программы задают последовательности операций, а универсальность обеспечивается тем, что любую алгоритмическую задачу можно свести к этим элементарным шагам. Классические вычислители опираются на булеву логику и последовательное исполнение команд. Соответственно, если для решения задачи размера n нужно совершить экспоненциально большее число операций (2n и больше), у классической машины быстро начнутся проблемы.
О «неклассических вычислениях» начали активно говорить в 1980-е годы, когда стало ясно: прогресса внутри фон-неймановской парадигмы может оказаться мало. Инженеры и физики стали искать альтернативные модели вычислений. Так что неклассические вычислители это большое множество, внутри которого есть как устройства, остающиеся в тьюринговой модели, так и те, что идут еще дальше.
Всерьез про «нейроморфные вычислители» заговорил Карвер Мид, когда предложил проектировать схемы на кремнии по образцу нейронных сетей. Здесь вычисления происходят в масcивно-параллельных сетях, результат которых — приближенный ответ. Чисто математически, это по-прежнему классическая аппроксимация функций и стохастическая оптимизация. То есть саму проблему экспоненциального числа шагов этот подход не отменяет, просто справляется в ряде случаев значительно быстрее.
Квантовые компьютеры — совсем другой случай. Здесь в дело вступает физика микромира: суперпозиция, интерференция и запутанность. Кубиты находятся в комбинации состояний 0 и 1, а несколько кубитов образуют вектор в гильбертовом пространстве. Благодаря этому меняется сама асимптотика сложности задачи. То, что на классике требует экспоненты (например, факторизация больших чисел), на квантовой схеме может решаться за полиномиальное время. Это не просто другой процессор, а другая модель вычислений. Класс сложности BQP шире классической вероятностной полиномиальной сложности (BPP).
Таким образом, если нейроморфные вычислители занимаются оптимизацией того, что уже достижимо, квантовые претендуют на то, чтобы пробить стену экспоненциальной сложности. То, что это возможно, окончательно стало ясно в 1994 году, когда возник алгоритм Шора и задача факторизации больших чисел стала полиномиальной на квантовой машине. С этого момента «классические» и «квантовые» вычисления стали противопоставляться как принципиально разные модели.
При этом универсального квантового вычислителя у нас нет, а его разработка продолжается вот уже 30 лет. Мы попросили Глеба Федорова перечислить, где в океане прямо сейчас находятся «острова квантового превосходства» и какие задачи можно решить строго квантованием.
Сэмплирование случайных квантовых схем (Random Circuit Sampling, RCS)
Хотя эта задача не имеет прямого практического применения, она является показательным тестом: современные квантовые компьютеры уже решают задачи, алгоритмически находящиеся далеко за пределами возможностей классических систем.
Работу Google 2019 года удалось превзойти с помощью кластеров GPU (и по скорости, и по энергопотреблению), последние результаты (Willow, Zuchongzhi-3) пока не имеют сопоставимой классической симуляции.

Сэмплирование бозонов (Gaussian Boson Sampling, GBS)
GBS также демонстрирует огромное превосходство квантовых устройств над классическим моделированием. Однако поскольку внутри таких процессоров нет четко определенных квантовых схем, правильнее рассматривать их как специализированные квантовые симуляторы.
Фотонные чипы решают похожую задачу. Например, известны эксперименты на китайской установке Jiuzhang (50–100 мод сжатого света) и канадском Xanadu Borealis (216 мод, 2022). В последнем случае оценка классической сложности составила ~9 тысяч лет.
Квантовая химия и материаловедение
Классические методы — теория функционала плотности (DFT), теория связанных кластеров (CC) — фундаментальны, но становятся вычислительно неприемлемыми для больших молекул и часто теряют точность при описании радикалов.
IBM Research и Lockheed Martin провели симуляцию молекулы CH₂ на 52-кубитном процессоре с использованием выборочного квантового диагонализатора (SQD). Получена энергия синглет-триплетного перехода (~19 милиХартри), согласующаяся с точными классическими расчетами и экспериментом. Молекула CH₂ известна своей трудностью для классических методов.
Другой пример — Fe₄S₄ кластер, который также неразрешим классическим методом. По оценкам IBM, даже отказоустойчивому квантовому компьютеру с ~4,53 млн кубитов потребуется ~13 дней для моделирования этой молекулы. Однако гибридные техники (SQD + классическая постобработка) могут давать полезные приближения куда эффективнее.
IBM также применяет расширенные модели Хаббарда и SQD к расчету запрещенных зон металлооксидов и сверхпроводников — задач, крайне сложных для классики, но критически важных для материаловедения.
Комбинаторная оптимизация
Многие NP-трудные задачи (логистика, финансы, машинное обучение) кодируются в гамильтонианы типа спиновых стекол и решаются с помощью вариационных или адиабатических методов.
IBM в 2025 году провела эксперимент на 156-кубитном сверхпроводниковом процессоре с алгоритмом BF-DCQO. Для некоторых синтетических HUBO-задач получены хорошие приближенные решения быстрее (по реальному времени), чем лучшие классические решатели (симулированный отжиг, CPLEX). Это также наглядная экспериментальная демонстрация квантового ускорения на специально подобранных трудных задачах.
Машинное обучение и квантовые вычислители
Активно изучается QML (quantum machine learning), совмещение квантовых алгоритмов и методов машинного обучения. Так, развиваются подходы, в которых квантовые операции оптимизируются подобно тому, как это происходит в алгоритмах машинного обучения (vQML). Уже известны случаи «деквантизации» задач: находился классический алгоритм, эффективность которого не уступает квантовым. Но это в принципе возможно лишь для некоторых типов задач.
Когда данные сами по себе — квантовые, преимущество квантового моделирования над классическими подходами доказано и экспериментально подтверждено. Квантовым моделям нужно меньше данных для эффективных предсказаний, чем любым классическим. В случае с применением квантовых алгоритмов к классическим данным, однако, вопрос о превосходстве остается открытым.

