Не каждый день удается поставить точку в решении математической задачи, имеющей многовековую историю. Хорошо известным примером такой задачи была гипотеза Ферма о неразрешимости в целых числах диофантового уравнения вида xn+yn=zn, при n>2. Гипотезу удалось доказать 30 лет назад. Также еще на слуху решение Григорием Перельманом проблемы Пуанкаре. Однако существует большое количество менее известных, но от этого не менее важных задач, имеющих многовековую историю. Одна из них восходит к Исааку Ньютону. В рукописи «Об анализе уравнениями бесконечных рядов» 1669 года он описал достаточно простую процедуру поиска решения уравнения f(x)=0 с помощью секущих (в современной терминологии касательных). Идея метода (рисунок 1) состоит в том, чтобы из текущей точки провести касательную к функции и в качестве нового приближения к решению взять пересечение этой касательной с осью абсцисс.
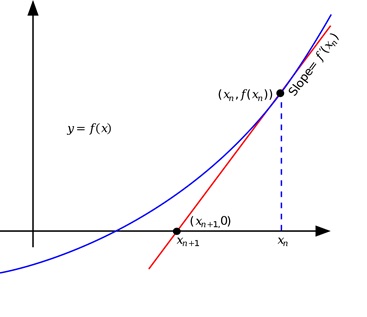
Рисунок 1. Идея метода «Секущих Ньютона»
Если функция f(x), в свою очередь, есть производная некоторой другой функции F'(x) = f(x), то предложенный Ньютоном метод секущих можно понимать как численный метод поиска экстремума, например точки минимума, функции F(x). Метод оказался очень эффективным на практике, однако он не всегда сходился. Отметим, что к развитию таких методов в позапрошлом веке приложил руку и выдающийся российский математик Пафнутий Львович Чебышевв, рассмотревший в своей дипломной работе возможные способы ускорения скорости сходимости метода Ньютона за счет использования старших производных целевой функции F(x). Существенным продвижением в анализе скорости сходимости метода Ньютона стали исследования советского математика, лауреата Нобелевской премии по экономике Леонида Витальевича Канторовича.
Оптимален ли метод Ньютона?
Несмотря на описанные выше замечательные исследования ведущих математиков своих поколений, вплоть до 1979 года было непонятно, насколько быстро в принципе можно находить минимум функции F(x), если в процессе ее оптимизации разрешается использовать ее производные, например первого и второго порядка. Под «насколько быстро» подразумевается следующее: если задаться желаемой точностью решения, то сколько раз потребуется посчитать производные целевой функции, чтобы найти минимум функции с заданной точностью. Понятно, что ответ будет зависеть от выбранного метода и от конкретной функции. Качество метода определяется тем, как он работает, то есть сколько вычислений производных требуется на худшей функции из рассматриваемого класса. Мы рассматриваем класс сильно выпуклых достаточно гладких функций.
Естественный вопрос, который интересовал ученых на протяжении многих веков: является ли метод Ньютона для класса достаточно гладких сильно выпуклых задач оптимизации наилучшим методом, использующим первые и вторые производные целевой функции, и если не является, то какой метод в таком случае будет оптимальным? Вопрос этот сложный, и до работы Аркадия Семеновича Немировского 1979 года было даже не совсем понятно, как правильно (математически строго) его поставить, чтобы можно было получить на него какой-то ответ. Грубо говоря, Немировским было показано, что метод Ньютона локально является оптимальным. Под «локально» имеется в виду, что точку старта метода нужно брать достаточно близко к решению. А что будет, если точку старта (начальное приближение) не удастся подобрать достаточно близко к решению? Ведь мы не знаем, где решение. Собственно, в этом же и задача — найти решение! Какой метод будет оптимальным без таких оговорок?
Данный вопрос активно исследовался в последние 20 лет. Важным продвижением в решении этого вопроса стала статья Нестерова — Поляка 2006 года, в которой авторы, используя простое наблюдение, что метод Ньютона (для задач оптимизации) можно понимать как метод, который на каждой итерации минимизирует квадратичную аппроксимацию целевой функции в данной точке, предложили перейти от квадратичной аппроксимации к кубической, добавив к квадратичной модели простой кубический член (регуляризатор). Этот подход получил название кубически регуляризованного метода Ньютона, или метода Ньютона — Нестерова — Поляка. Предложенный метод уже глобально сходился к решению, но лишь локально проявлял нужные оптимальные свойства. То есть задача по-прежнему не была решена.
В 2013 году Монтейро — Свайтер предложили универсальный способ ускорения различных методов оптимизации и продемонстрировали свой подход в том числе на методе Ньютона. Как оказалось, авторы «почти» решили поставленную задачу. Однако на тот момент было непонятно, насколько хороших оценок глобальной скорости сходимости стоит ожидать, поскольку не были известны нижние оценки возможной глобальной скорости сходимости.
Первые нижние оценки появились только в 2017 году. Собственно, приблизительно тогда и стало понятно, что метод Ньютона, завернутый в ускоренную оболочку Монтейро — Свайтера, оптимален (сходится, согласно нижним оценкам, а это значит, что не существует в общем случае более быстрого метода для данного класса задач), с точностью до логарифмического по желаемой точности множителя в оценки сложности метода. Этот логарифмический множитель связан с процедурой одномерного поиска, которая в целом затрудняет не только теоретический анализ метода, но и его практическое использование.
Финишная прямая
В 2018 году наш выдающийся современник, лауреат премий Данцига и фон Неймана, один из основателей современной оптимизации Юрий Нестеров поставил задачу — устранить это логарифмический зазор между известными нижними оценками и оценками, достигаемыми существующими методами (к 2018 году таких методов появилось уже четыре). По сути, речь была о том, как убрать одномерный поиск в подходе Монтейро — Свайтера. Ученые во всем мире активно взялись за решение этой задачи. В том числе и сам Нестеров активно работал в этом направлении, написав вокруг данной темы к настоящему моменту уже около 20 статей. Однако вплоть до мая 2022 года проблема так никому и не поддавалась.

Рисунок 2. Демонстрация того, что метод Ковалева лучше не только в теории, но и на практике
В мае 2022 года один из наиболее ярких студентов своего поколения — Дмитрий Ковалев, аспирант ИППИ РАН и сотрудник лаборатории методов математической оптимизации МФТИ, который в свое время дважды становился лауреатом премии Ильи Сегаловича и награды за лучшую статью на воркшопе ICML 2021, полностью решил данную задачу. Он предложил оптимальный метод, который сходится в точности по нижним оценкам. Удалось этого добиться, как и предвидел Юрий Нестеров, за счет правильного устранения одномерного поиска в процедуре Монтейро — Свайтера. Но на понимание того, как это сделать, ушло четыре года. Может показаться, что все это чисто математические упражнения, которые не так важны для практики. Однако Ковалев показал, что его подход заметно выигрывает и на практике в два раза быстрее сходится на рассмотренных задачах, что можно видеть на рисунке 2. Но, что еще более важно, в подходе Ковалева предложен вполне обычный метод оптимизации, который относительно просто исследовать (по сравнению с методом Монтейро — Свайтера), обобщать и развивать. В работе, которую Дмитрий Ковалев представил на конференции NeurIPS 2022, были предложены оптимальные методы и в классе алгоритмов, которые допускают использование старших производных любого порядка.
Побочные продукты решения
Чем примечательна данная история? На наш взгляд, она довольно типична для развития той или иной области науки. Есть какая-то яркая и понятная задача, которая мотивирует (будоражит умы) специалистов в данной области. Часто важность задаче придают попытки участия в ее решении ведущих специалистов. Как правило, задача не решается сразу и по ходу ее решения рождаются новые теории, подходы, которые сами по себе бывают даже более ценными, чем сама конкретная задача, которая примечательна только тем, что компактно сформулирована и содержит в себе основные сложности, преодолев которые удастся много чего еще сделать… В какой-то момент в попытке решения данной задачи накапливается достаточно много критически важных результатов, и решение неизбежно случается, причем случается независимо и сразу в нескольких местах (задачу решают практически одновременно разные группы ученых, причем, как правило, по-разному). В аспирантских курсах философии и истории науки это наблюдение приписывают Гегелю.
Например, в решении проблемы Ферма «побочным» продуктом стало создание теории эллиптических кривых, которые изначально развивались как некая вещь в себе, возможно, полезная для решения проблемы Ферма… Но впоследствии эллиптические кривые кардинальным образом преобразили в высшей степени практические разделы криптографии (теории кодирования). Собственно, так и в нашей истории: предложенные в 2018 году Юрием Евгеньевичем Нестеровым тензорные методы третьего порядка, появившиеся на свет как реакция на описанную задачу, на наш взгляд, совершили своего рода революцию в современных численных методах оптимизации. Об этом наверняка еще будут написаны отдельные статьи, популяризирующие данную находку. Если обобщить, Нестеровым было подмечено, что класс методов оптимизации, использующих производные первого и второго порядка целевой функции, в некотором смысле неполный, следовательно, с точки зрения глобальной сходимости разумно использовать методы третьего порядка (говорят также «тензорные методы третьего порядка»), которые используют все производные целевой функции вплоть до третьего порядка включительно. Главным наблюдением Юрия Нестерова было, что при весьма общих предположениях о семействе допустимых методов, в котором ищется оптимальный, стоимость итерации таких методов практически не отличается от стоимости итерации метода Ньютона, в котором на каждой итерации требуется решать специальную систему линейных уравнений. Другими словами, несмотря на то, что несколько веков ученые заостряли свое внимание на методе Ньютона, оказалось, что можно построить намного более быстрые методы (в смысле скорости глобальной сходимости), если разрешить использовать производные целевой функции третьего порядка. При этом трудозатратность итерации у таких методов будет практически такая же, как и у метода Ньютона. То есть такие методы значительно быстрее по времени в итоге будут решать задачи оптимизации.
Джентльмены науки
Как и следует по Гегелю, в нашей истории решение задачи «в родничок упало» не только Дмитрию, но также, практически одновременно, группе американских ученых из Стэнфорда во главе с Аароном Сидфордом. Здесь полезно упомянуть другую поучительную историю, связанную с тем, как в такой ситуации можно себя вести. Американские коллеги так же, как и Дима, готовили статью на конференцию NeurIPS 2022. Но Дмитрий выложил свою статью на arXiv 19 мая и был первым. Увидев там публикацию Ковалева, американские коллеги поняли, что у них остается буквально пара дней до дедлайна, чтобы внести в свою статью правку. Они корректно это сделали, сославшись на то, что один из их главных результатов был получен в статье Дмитрия Ковалева. Вообще говоря, такое замечание серьезно снижает вероятность прохождения статьи, и авторы не могли этого не понимать. Но они поступили честно: раз увидели, надо сослаться. Статья Сидфорда и соавторов в итоге также прошла на NeurIPS 2022. Авторы написали Диме письмо и рассказали про все это. Естественно, Дмитрий в итоговой версии своей статьи также добавил ссылку на то, что аналогичный результат независимо, но другим способом был получен коллективом из Стэнфорда. Кажется, это хороший пример того, как можно разрешать такого рода ситуации. Ведь в данной истории все себя проявили достойно: и авторы двух статей, и рецензенты, которые с пониманием отнеслись к возникшей ситуации. Отмечу, что подобные истории возникают довольно часто, и, к счастью, довольно часто они решаются именно таким образом. Не многолетней борьбой за приоритеты, а мирным разделением своего успеха с коллегами.

Дмитрий Ковалев, аспирант ИППИ РАН и сотрудник лаборатории математических методов оптимизации МФТИ
Пара мыслей про фундамент и развитие
В завершение сюжета хотелось бы выделить из канвы повествования две мысли, которые явно не прозвучали до сих пор. Одну мысль можно адресовать чиновникам от науки, а вторую — молодежи, собирающейся заниматься наукой.
Итак, из всего вышенаписанного можно сделать такой вывод: работая над решением, в общем-то, фундаментальной задачи Юрия Евгеньевича Нестерова, Дима и многие другие герои нашего сюжета, насколько мне известно, не искали прямых приложений. Они не пытались сделать новый прибор или решить какую-то конкретную практическую задачу. Можно сказать, что перечисленные ученые просто занимались математикой (своей основной специальностью), развивая определенную область — тензорные методы оптимизации. Решив исходную задачу (далекую, на первый взгляд, от каких-то конкретных приложений), они получили большое число чисто научных результатов, которые позволили впоследствии другим людям не только получить ряд хороших практических методов, но и запустить целую индустрию тензорных методов распределенной оптимизации. Например, на такую «распределенно-тензорную» технологию недавно перешла компания Yahoo! в части обучения click-prediction model. Особенно перспективным все это видится в сочетании с популярной сейчас технологией федеративного обучения, в которой задачи квадратичной (стохастической) оптимизации решаются особенно эффективно в смысле числа коммуникаций. А ведь именно такие задачи квадратичного типа как раз и возникают как вспомогательные в практичных версиях развиваемых в последнее время тензорных методов на каждой их итерации. Так вот, очень важной составляющей работы таких ученых-«фундаменталистов» 🙂 является поддержка их фундаментальных исследований. Насколько нам известно от коллег, во всех странах мира с этим есть проблемы. И чем дальше, тем проблем больше. Деньги вкладываются в ожидании конкретных результатов. А сюжеты, подобные тому, который описан в данной заметке, весьма характерны в целом для развития многих областей науки. Понимание и учитывание таких особенностей развития науки, возможно, позволят еще лучше организовывать спонсирование научных коллективов.
В преддверии описания второй мысли заметим, что на данный момент Дима Ковалев сотрудничает с Юрием Евгеньевичем Нестеровым и сейчас они уже вместе взялись за развитие данной области. Это тоже очень хороший и в некотором смысле типичный пример того, что современная наука — это не только собственные достижения, но и правильная коллаборация, сотрудничество. Видится, что коллаборация в современной науке начинает играть ту же роль, что и симбиоз в образовании эукариотических клеток, выходе растений на сушу и последующем многократном и многослойном росте сложности живых организмов вместе с их расширенным фенотипом в окружающем нас мире. Иными словами, как в анекдоте про льва, зайца и волка: «не важно какая тема, важно, кто научный руководитель» 🙂 Это, конечно, всего лишь анекдот, но доля правды, по-видимому, в нем есть. Чтобы достичь вершины, нужно выбирать правильного гида / научного руководителя / соавторов, которые сократят ваш путь к последнему базовому лагерю / переднему краю науки, чтобы у вас остались силы и мотивация все-таки дойти до вершины и вернуться, чтобы взойти на еще много новых вершин и подготовить следующие поколения альпинистов / математиков 🙂
Литература
- Kovalev D., Gasnikov A. The First Optimal Acceleration of High-Order Methods in Smooth Convex Optimization // NeurIPS – 2022.
- Carmon Y. et al. Optimal and Adaptive Monteiro-Svaiter Acceleration // NeurIPS – 2022.
- Kamzolov D. et al. Exploiting higher-order derivatives in convex optimization methods // arXiv preprint arXiv:2208.13190. – 2022.
- Nesterov Y., Polyak B. T. Cubic regularization of Newton method and its global performance // Mathematical Programming. – 2006. – V. 108. – №. 1. – P. 177-205.
- Nesterov Y. Implementable tensor methods in unconstrained convex optimization // Mathematical Programming. – 2021. – V. 186. – №. 1. – P. 157-183.
- Dvurechensky P. et al. Hyperfast second-order local solvers for efficient statistically preconditioned distributed optimization // EURO Journal on Computational Optimization. – 2022. – V. 10.
- Bullins B. et al. A Stochastic Newton Algorithm for Distributed Convex Optimization // Advances in Neural Information Processing Systems. – 2021. – V. 34. – P. 26818-26830.
- Немировский А.С., Юдин Д.Б. Сложность задач и эффективность методов оптимизации. М.: Наука – 1979.
- https://github.com/OPTAMI/OPTAMI
10

