Ученые из МФТИ и НИУ ВШЭ разработали суперкомпьютерный метод моделирования жидкости на атомных масштабах, позволяющий описывать возникновение турбулентных режимов течения. Максимизировав скорость вычислений новым методом, ученые рассчитали на суперкомпьютере течение жидкости, состоящей из нескольких сотен миллионов атомов. Новый метод пригодится для понимания и корректного описания процесса диффузии в турбулентном потоке и особенностей турбулентного течения жидкости возле стенок. Разработанный метод уже применяется для моделирования течения жидкометаллического свинцового теплоносителя в ядерном реакторе. Работа опубликована в The International Journal of High Performance Computing Applications.
В компьютерном моделировании жидкость обычно описывают как сплошную среду, лишенную дискретности, а ее течение определяют с помощью численного решения дифференциальных уравнений Навье — Стокса. Такие модели называются континуальными, и в них не описывается поведение отдельных атомов и молекул жидкости. В прикладных задачах ученых очень часто интересует не спокойное — ламинарное, а турбулентное течение, когда потоки жидкости образуют вихри разного размера, меняющиеся во времени и пространстве стохастически. В 1940-е годы советский математик, академик Андрей Николаевич Колмогоров создал теорию эволюции вихрей в турбулентных потоках, показав, что большие вихри измельчаются в маленькие вплоть до десятков и сотен нанометров. При таких размерах (на «Колмогоровском масштабе длины») континуальные методы не работают, так что нужно моделировать поведение отдельных атомов и молекул, численно решая их уравнения движения. Переход к подобному дискретному описанию может быть критически полезен для некоторых специальных случаев. Например, так можно изучать диффузию и образование кластеров частиц в турбулентном потоке. Конечно, эти процессы можно рассматривать в континуальном приближении, однако корректность используемых допущений можно проверить только с помощью атомистического моделирования.
Для изучения зарождения турбулентности ученые из МФТИ и НИУ ВШЭ разработали концепцию, позволяющую наблюдать быстрое течение жидкости, огибающей препятствия, на микрометровых масштабах. Сначала ученые придумали способ, как удержать поток жидкости в ограниченных размерах, затем реализовали его в двух программах для молекулярного моделирования. В третьей части работы исследователи проанализировали производительность суперкомпьютеров, на которых проводились расчеты, и пути ее оптимизации.
Руководитель научной группы, выполнившей работу, заведующий отделом ОИВТ РАН, заведующий лабораторией суперкомпьютерных методов в физике конденсированного состояния МФТИ и ведущий научный сотрудник Международной лаборатории суперкомпьютерного атомистического моделирования и многомасштабного анализа НИУ ВШЭ Владимир Стегайлов рассказывает: «Наша фундаментальная мотивация была в том, чтобы увидеть процессы, связанные с турбулентностью: образование вихрей, диффузию, формирование и растворение кластеров атомов на том масштабе, который принципиально невидим в рамках описания методами сплошной среды, то есть не на сетке, а непосредственно решая уровень движения атомов и молекул. Мы получили естественный поток жидкости с завихрениями, которые возникают сами собой в результате обтекания препятствия на масштабах в сотни миллионов атомов, чего до нас еще не делали. Цель нашего нового метода — получать данные для особых случаев, таких как диффузия, течение возле стенок, чтобы физически правильно сопрягать атомный и континуальный масштаб в тех областях моделирования, где эта смычка является критической важной».
Моделируемая система представляла плоский квазидвумерный параллелепипед, внутри которого находились цилиндрическое препятствие и от нескольких миллионов до нескольких сотен миллионов атомов жидкости. К тепловым скоростям атомов добавлялась заданная скорость потока, и если она была достаточно большой, то после огибания цилиндра спонтанно формировались турбулентные вихри. Так ученые смогли в естественных условиях промоделировать возникновения предтурбулентного режима течения, не накладывая на движение жидкости иных специальных условий.
Сложность моделирования состояла в том, что частицы в процессе движения должны покидать пределы параллелепипеда. Обычно в атомистическом моделировании применяют периодические граничные условия, когда атомы, условно покинувшие систему справа, на следующем шаге расчетов искусственно возвращаются в систему слева с той же скоростью и направлением движения. Таким образом, система остается замкнутой. Этот метод наиболее вычислительно простой. В задаче с вихрями физикам пришлось придумать такие периодические условия, чтобы при переходе границы системы течение переставало быть турбулентным, иначе после возвращения покинувших атомов в параллелепипед налетающая на препятствие жидкость уже была бы турбулентной, что нарушило бы постановку задачи. Ученые предложили расположить возле правой границы системы виртуальные плоскости, после пересечения которых скорость частиц перерассчитывалась, течение становилось нормальным (ламинарным), а значит, возвращение атомов не нарушало условие ламинарности натекающего потока.

На рисунке изображена ячейка моделирования в боковой проекции. Белым цветом обозначено цилиндрическое препятствие. Более синие участки соответствуют большей плотности частиц, светлые — меньшей плотности. Видно, что после прохождения препятствия возникают завихрения, характеризующиеся разной плотностью частиц. Также справа заметны плоскости, после пересечения которых происходит перераспределение скоростей частиц и поэтапная ламинаризация потока. Источник: The International Journal of High Performance Computing Applications
Видео. Ячейка моделирования с 230 миллионами атомов в боковой проекции. Цвет показывает локальную плотность частиц. Более синие участки соответствуют большей плотности частиц, светлые — меньшей плотности. Видно, что после обтекания цилиндра в потоке образуется стохастическая вихревая дорожка Кармана. Также справа заметны плоскости, после пересечения которых происходит перераспределение скоростей частиц и поэтапная ламинаризация потока
После теоретического обоснования предложенных граничных условий ученые внедрили их в широко используемые программы для молекулярного моделирования LAMMPS и OpenMM и рассчитали течение жидкости на суперкомпьютерах с графическими ускорителями. Отдельное внимание ученые уделили сохранению максимальной производительности вычислений, поскольку в системах из миллионов атомов, для которых рассчитывается несколько миллионов временных шагов, миллисекундное ускорение на одном вычислительном шаге приводит к экономии нескольких дней и даже недель работы суперкомпьютера.
Студент магистратуры ЛФИ МФТИ Даниил Павлов, первый из двух главных авторов статьи, отмечает: «Возможность достичь столь высокой скорости расчетов, которую мы продемонстрировали в нашей работе, достигается за счет переноса вычислений на графические ускорители. На курсе алгоритмов нас учат оценивать асимптотическую сложность алгоритмов. Нас учат рассуждать, каким образом время исполнения программы будет расти при росте тех или иных параметров входных данных: линейно, квадратично, экспоненциально? В первое время может сложиться впечатление, что все хоть сколько-то значительные оптимизации заключаются в улучшении асимптотической сложности алгоритма, а все остальное — микрооптимизации, выжимающие лишь последние несколько процентов производительности. Естественно, многие программисты понимают, что в реальности все не так просто, но легко недооценить возможный прирост производительности. Грамотно написанный и распараллеленный код может обгонять референсную, неоптимизированную реализацию в сотни или даже тысячи раз, особенно если использовать графический ускоритель. Вычисления, которые раньше занимали день, теперь занимают пару минут. Вычисления, которые раньше занимали год, теперь укладываются в пару дней. Все, что нужно, — грамотно написанный алгоритм и современное (даже необязательно дорогое) железо. Для меня само существование возможности заставить алгоритм, даже изобретенный уже несколько десятков лет назад, работать на несколько порядков быстрее, кажется крайне удивительным».
Студент магистратуры МИЭМ НИУ ВШЭ Владислав Галигеров, второй из двух главных авторов статьи, добавляет: «Как многим, наверное, известно, закон Мура уже примерно лет десять как перестал выполняться: число транзисторов уже не удваивается каждые два года, в этом плане прогресс замедлился. Поэтому упор все больше делается на многоядерность, ускорение работы с памятью, программные оптимизации и “передачу” вычислений с центрального процессора на специализированные устройства вроде графических ускорителей (по-английски последнее называется computation offloading). В связи с этим все чаще в области суперкомпьютерных вычислений встает вопрос о переносимости производительности: будет ли данная программа, собранная и протестированная на одной системе, так же хорошо работать на другой? При этом бывает полезно не только увидеть общие цифры (то есть сколько по времени запускалась программа или отдельная функция), но и посмотреть на расчет в динамике и “вглубь”: сколько данных было передано между узлами, процессорами и GPU, как часто это происходило, сколько было промахов кэша и т. д., а также оценить эффективность распараллеливания. Ситуация осложняется тем, что многие программные пакеты, с которыми мы часто работаем, имеют огромный размер в несколько сотен тысяч строк кода. Множество людей делают свой вклад в какой-то один проект, и бывает сложно проанализировать всю картину целиком. Поэтому сейчас все больше развиваются инструменты для такого глубокого анализа производительности, например инструмент анализа параллельных программ Score-P, который мы использовали в данной работе. Очень важно выработать стандарты работы с такими инструментами, чтобы разработчики программ для суперкомпьютеров, внося изменения в существующий код или написав что-то новое, могли провести анализ в соответствии с ними и оценить, насколько эффективным будет их приложение на различных архитектурах суперкомпьютеров, включая те, к которым они не имеют доступа».
Владимир Стегайлов подчеркивает: «Ускорить расчет — значит как будто увеличить наш суперкомпьютер. Это можно выразить в рублях: если суперкомпьютер условно стоит 20 миллионов, а в результате оптимизации расчет проходит в два раза быстрее, то мы 20 миллионов сэкономили. При этом часто факторы, влияющие на производительность, скрыты от пользователя, у него нет простых способов понять, что вычислительные ресурсы задействованы максимально эффективно. Бывает так, что расчет идет корректно, но в 10 или в даже в 100 раз медленнее, чем мог бы идти на данной вычислительной системе. Лет десять назад я понял, что специалистов, которые могут помочь разобраться в этих проблемах, очень мало. Поэтому мы с моими коллегами начали досконально вникать во все научно-технические проблемы, связанные с эффективностью суперкомпьютерных вычислений. Очень важно развивать культуру пользования суперкомпьютерами. Дело осложняется тем, что технологии быстро эволюционируют».
В третьей части работы ученые анализировали производительность суперкомпьютеров, использованных для вычислений: для анализа они использовали суперкомпьютеры «Десмос» в Объединенном институте высоких температур РАН и «HARISMa» в НИУ ВШЭ. Основная часть расчетов производится на графических процессорах (GPU), при этом важно, чтобы они быстро обменивались данными в процессе расчета. Ученые показали, что ключевую роль в ускорении расчета играет механизм обмена данными между GPU. Если обмены проходят, минуя центральный процессор, который выполняет только управляющую роль, то скорость счета может возрасти в три раза! Также ученые построили временные развертки (трейсы) работы программы, по которым можно отследить последовательность выполнения отдельных функций, в частности, увидеть, какое время тратится на обмены данными между GPU-ускорителями. Такой анализ полезен для понимания того, где происходит замедление работы программы, и для последующей оптимизации расчетов.
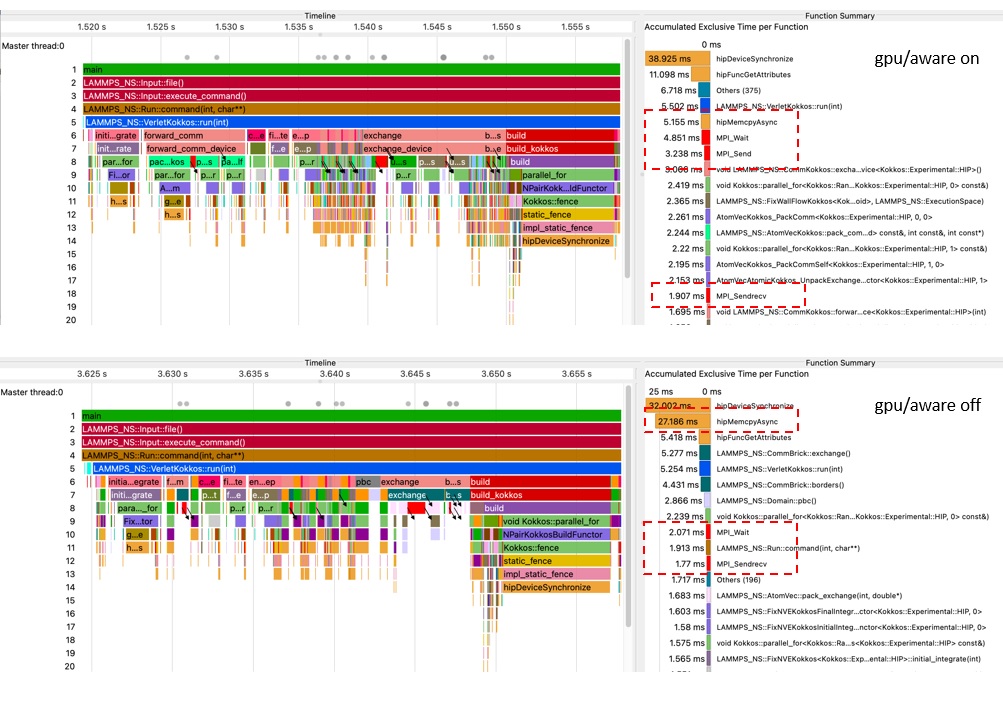
Примеры временной развертки (трейсов) для двух случаев работы молекулярно-динамического пакета LAMMPS: с использованием технологии обмена данными GPU-aware MPI и без нее. Видно существенное сокращение времени копирования данных в вызове hipMemcpyAsync. Неожиданный эффект, показанный авторами в статье, заключается в том, что суммарное ускорение вычислений в LAMMPS за счет использования технологии GPU-aware MPI составляет три раза. Источник: The International Journal of High Performance Computing Applications
Ученые уже применяют новый атомистический метод моделирования элементов турбулентности, чтобы описать течение свинца в ядерных реакторах на быстрых нейтронах. Жидкий свинец в стальных трубках используется в качестве теплоносителя, при этом течение сильно турбулентное. Важно понимать, как происходят взаимодействие свинца со стальными стенками, их коррозия и эрозия, в том числе диффузия кислорода в свинце и образование твердых оксидных частиц. Молекулярное моделирование позволит проверить корректность континуальных моделей, используемых для изучения подобных процессов в теплоносителе.
Владимир Стегайлов обобщает: «Данный тип задач, когда мы из масштаба молекулярной динамики пытаемся описывать какие-то мезоскопические явления в потоках, требует больших суперкомпьютеров. Таких задач, требующих очень большого числа одновременно используемых ресурсов, на самом деле не так уж много. Можно сказать, что получается замкнутый круг: пока нет больших суперкомпьютеров, ученые и не думают о такого уровня задачах, а раз они не думают, значит, не выражают потребности использовать большие суперкомпьютеры и не готовы к сопутствующим техническим вызовам. Мы пытаемся разорвать этот круг в своей работе, показываем, что даже на тех суперкомпьютерных ресурсах, которые у нас есть, мы умеем максимально эффективно решать большие вычислительные задачи, имеющие и фундаментальное научное значение, и важные прикладные последствия. Мы уже используем предложенный метод для описания протекания жидкометаллического теплоносителя, что важно для решения задач, которые ставит перед нами “Росатом”. Очень хотелось бы получить доступ на имеющиеся в России суперкомпьютеры в 10–40 раз большего размера, такие как у МГУ, “Яндекса” и “Сбера”, чтобы попробовать использовать наш алгоритм в большем масштабе для исследования трехмерной турбулентности. Мы готовы к этим расчетам».

