Коллектив ученых проанализировал эффект выделения тепла в проводнике под воздействием электрического тока для углеродных нанотрубок и пришел к выводу, что обычная теория плохо применима. Оказалось, что формула Мотта не работает, но применима формула Кельвина. Работа опубликована в журнале Physical Review B.
Несмотря на то, что углеродные нанотрубки были открыты почти 20 лет назад, изучение этой формы углерода продолжает оставаться актуальной темой как в экспериментальной, так и в теоретической науке. Разнообразные исследования показали, что углеродные нанотрубки обладают уникальными физическими свойствами, которые могут быть применены в различных сферах человеческой деятельности, таких как микроэлектроника, биомедицина, конструирование прочных структур и создание нанодвигателей. В связи с этим интерес представляет изучение всех классических физических эффектов для нанотрубок.
Еще с XIX века физики хорошо знакомы с эффектом Зеебека, который заключается в создании разности потенциалов (напряжения) в проводнике из-за перепада температур. Это напряжение, также известное как термоЭДС, пропорционально разности температур в проводнике. Однако исследователи обнаружили, что для одномерных систем типа «углеродная нанотрубка», где электроны двигаются в баллистическом режиме, возникающая разность потенциалов имеет отличное от предсказанного теорией Мотта значение.
Коэффициент Зеебека равен отношению электрического напряжения к разнице температур между двумя точками электрического проводника. При изучении этого эффекта электроны рассматривают как волны, перемещающиеся по материалу. Главную роль в их описании играет закон дисперсии — зависимость энергии электрона от пространственной частоты его движения, то есть волнового числа, равного отношению двух пи к длине волны. Для вычисления коэффициента Зеебека вид этой зависимости имеет огромное значение.
Например, закон дисперсии электронов в графеновой нанотрубке является линейным при квантовом числе j = 0 и параболическим при j = +-1. Это квантовое число характеризует вращательный момент электрона.
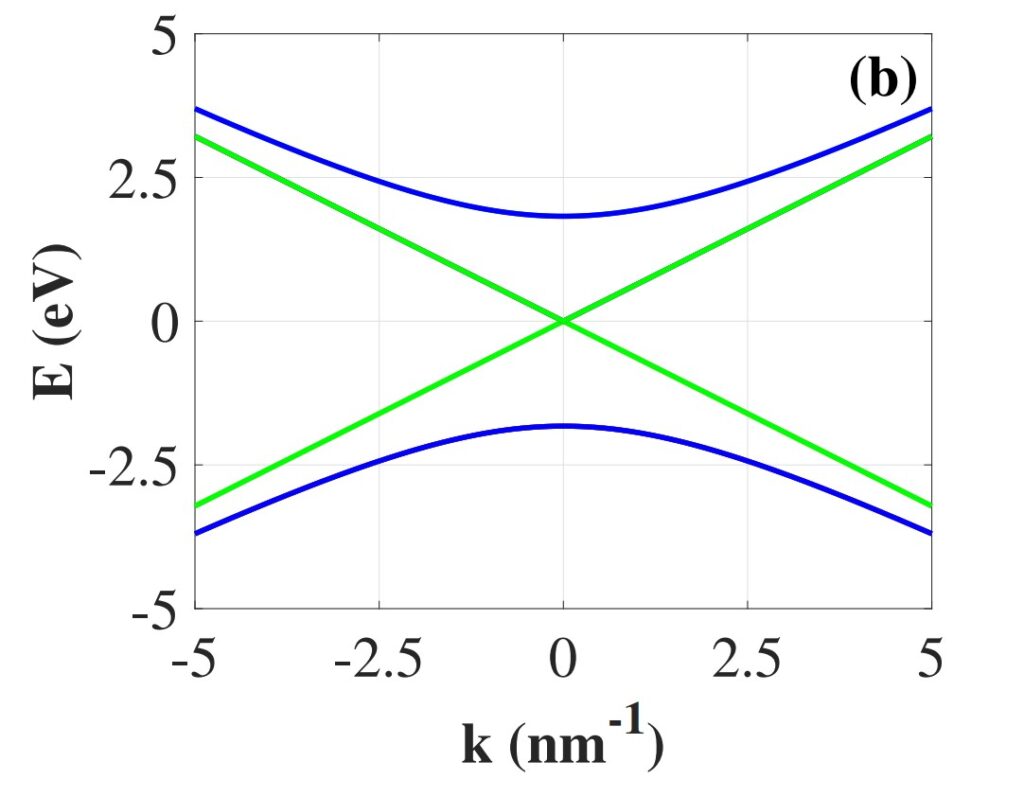
Рисунок 1. Закон дисперсии для электрона в углеродной нанотрубке. Зеленая линия соответствует квантовому числу j = 0, верхняя синяя линия j = 1, а нижняя синяя линия соответствует j = — 1. Источник: Physical Review B
Когда закон дисперсии мало отличается от линейного, теория Мотта справедлива. Но в реальных графеновых нанотрубках при комнатной температуре энергия движения электронов такова, что закон дисперсии правильнее описывать параболой. Случай, когда электроны не испытывают рассеяния при движении, называется режимом баллистического транспорта. Перенос тепла такими «баллистическими» электронами имеет ряд интересных особенностей.
В результате вычислений, проведенных группой ученых под руководством Алексея Кавокина, директора Международного центра теоретической физики имени А. А. Абрикосова МФТИ, оказалось, что значение коэффициента Зеебека от предсказанного теорией Мотта заметно отличается уже при температуре 77 кельвинов (то есть минус 196 градусов по Цельсию), а при температурах, близких к комнатным, теория Мотта неприменима.
Физикам удалось показать, что в этих случаях намного более точно описывает эффект теория Кельвина, которая предсказывает выражение для коэффициента Зеебека на основе термодинамических соображений.
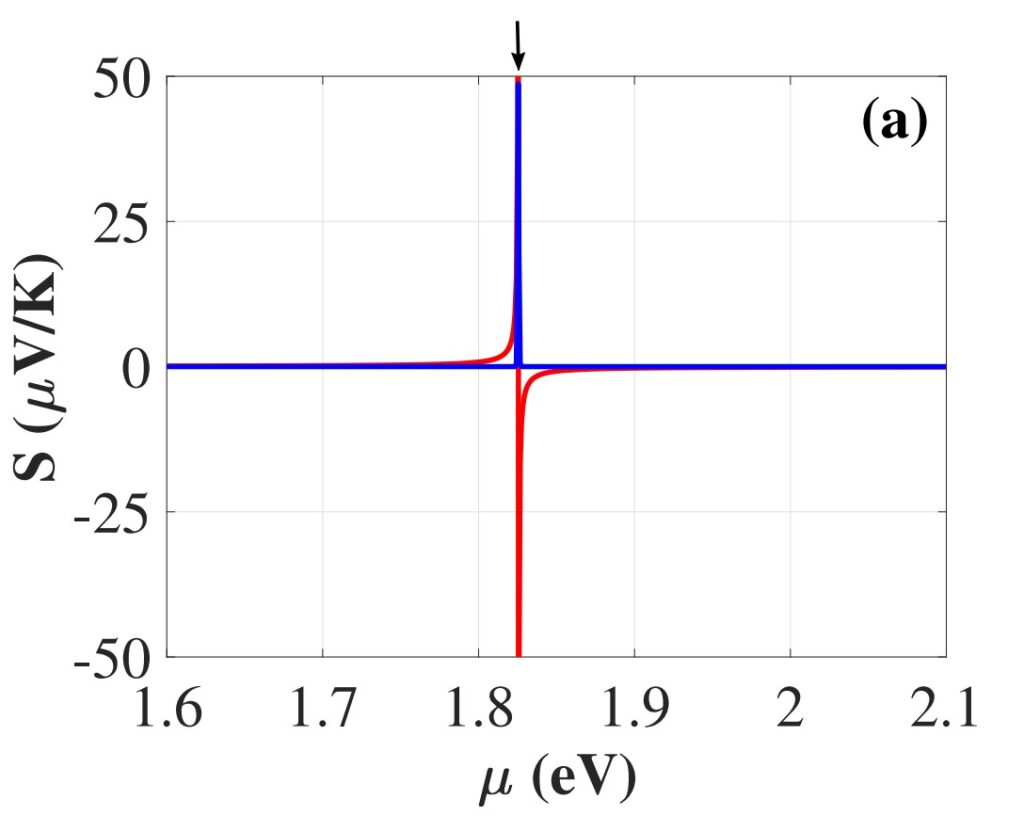
Рисунок 2. Зависимость коэффициента Зеебека от химического потенциала при температуре 2,4 кельвина. Значение по формуле Мотта изображено синей линией, а результат намного более точной для данной системы формулы Кельвина — красной линией. Источник: Physical Review B
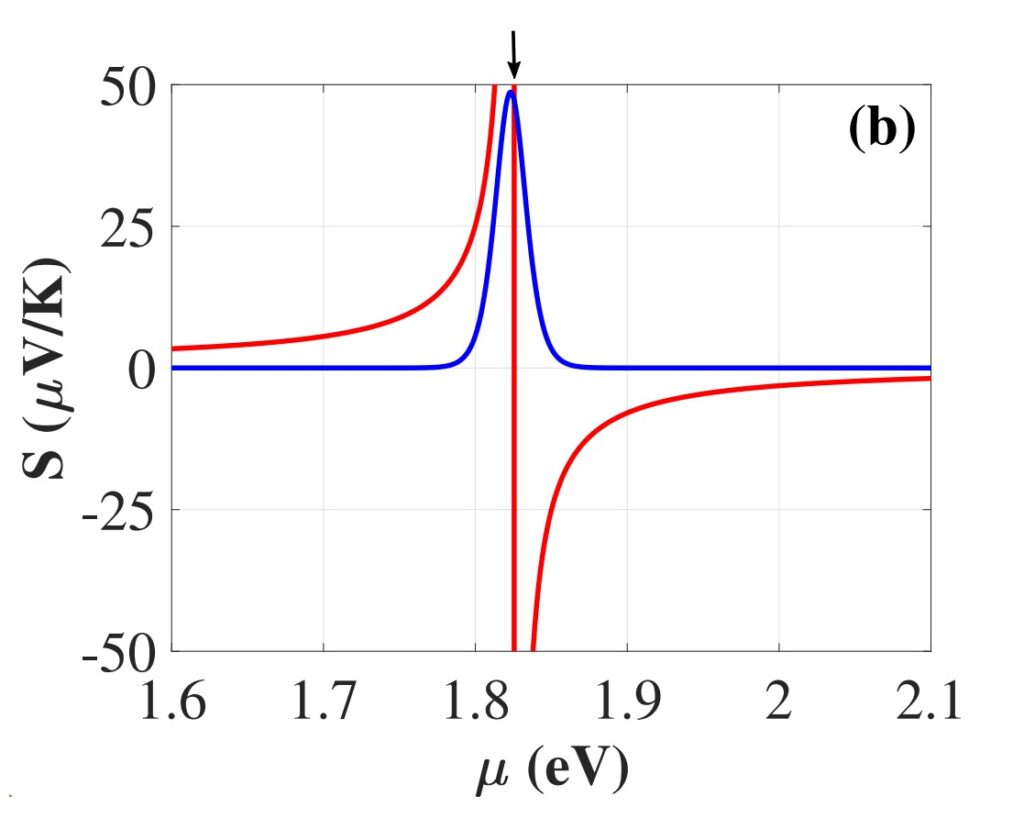
Рисунок 3. Зависимость коэффициента Зеебека от химического потенциала при температуре 77 кельвинов. Значение по формуле Мотта изображено синей линией, а результат намного более точной для данной системы формулы Кельвина — красной линией. Источник: Physical Review B
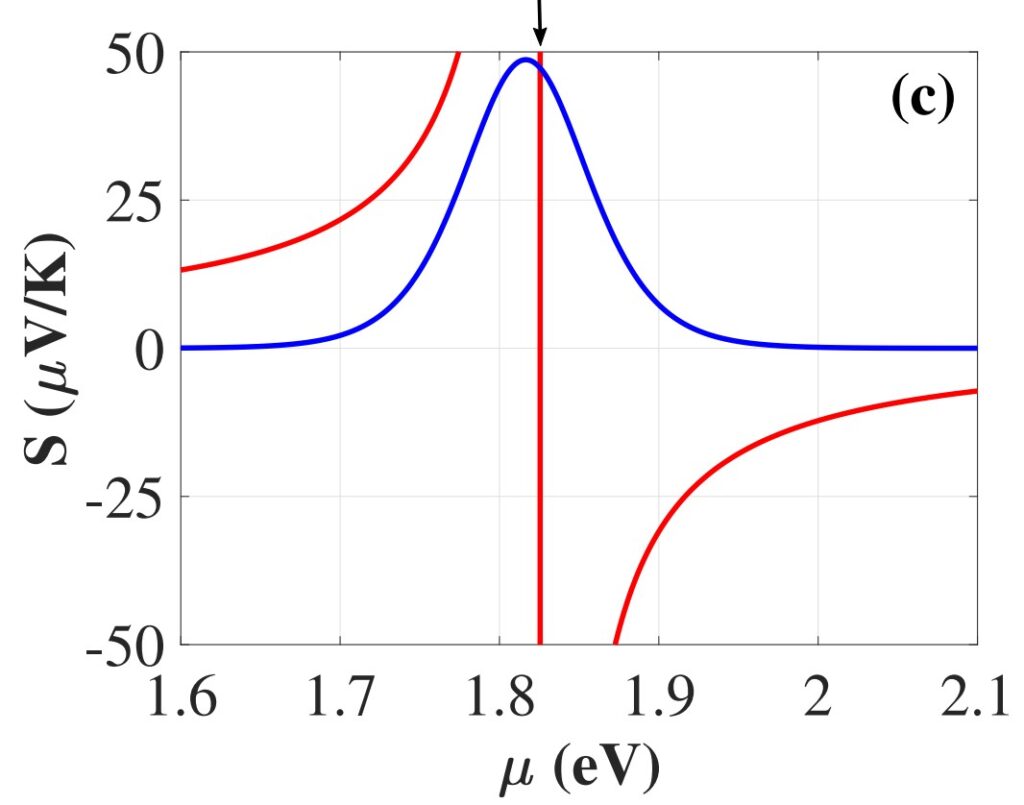
Рисунок 4. Зависимость коэффициента Зеебека от химического потенциала при температуре 300 кельвинов. Значение по формуле Мотта изображено синей линией, а результат намного более точной для данной системы формулы Кельвина — красной линией. Источник: Physical Review B
Кроме того, при любых температурах существует огромная принципиальная разница в результатах, полученных с помощью подхода Кельвина и подхода Мотта. Подход Кельвина предсказывает гиперболический спад коэффициента Зеебека вдали от резонанса между химическим потенциалом и дном энергетической подзоны. В точке резонанса наблюдаются сингулярность и смена знака коэффициента Зеебека. Напротив, формула Мотта предсказывает конечное значение коэффициента Зеебека на дне подзоны размерного квантования, отсутствие смены знака и быстрый экспоненциальный спад вдали от резонанса. Таким образом, даже при низких температурах эти две зависимости существенно отличаются как при приближении к точке резонанса, так и при большом удалении от нее: экспоненциальный спад намного быстрее гиперболического.
В любой реалистичной одномерной системе эти зависимости размываются из-за множества факторов: от эффектов конечного размера до флуктуаций и нелинейностей. Поэтому ученые решили учесть также эффект размазывания, введя для этого отдельный специальный параметр тау, имеющий размерность времени.
Оказалось, что эффект размазывания приближает предсказания обеих теорий (Мотта и Кельвина) друг к другу, делая теорию Мотта более точной.
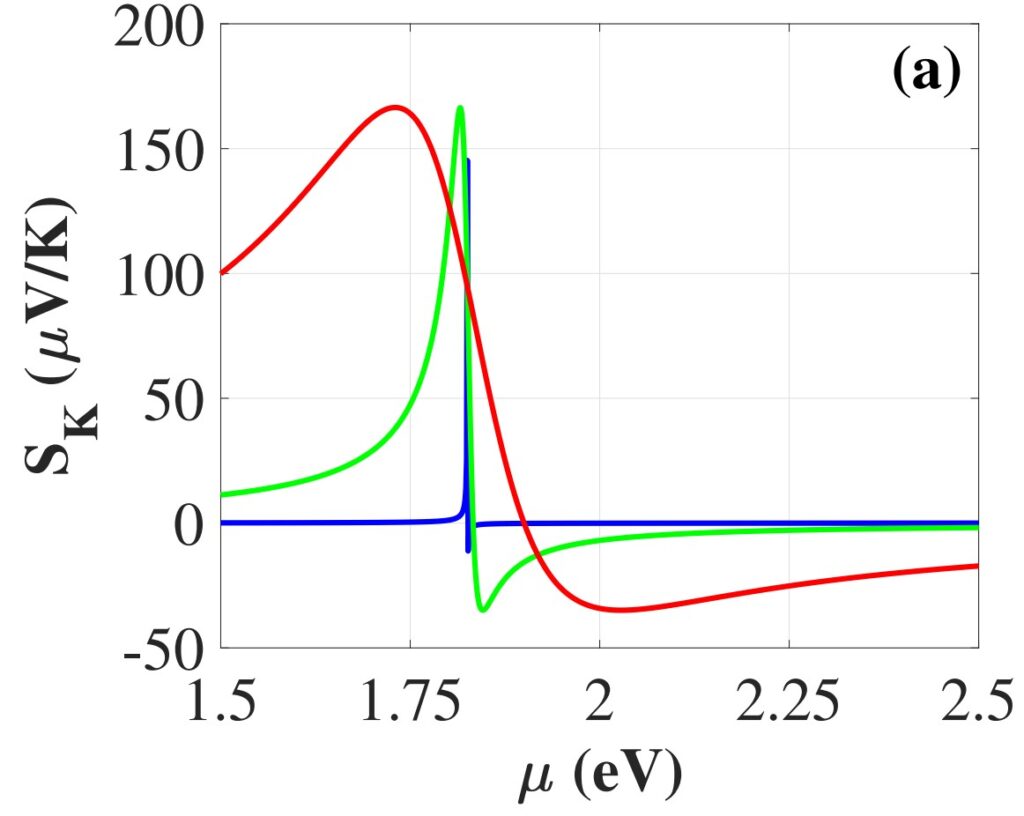
Рисунок 5. Зависимость коэффициента Зеебека от химического потенциала для параболического закона дисперсии при квантовом числе j = 1, вычисленная в теории Кельвина, при разных значениях параметра размазывания: τ /ℏ=483.09 eV^(-1) соответствует синему графику, τ /ℏ=38.65 eV^(-1) — зеленому графику и τ /ℏ=3.86 eV^(-1) — красному графику. Источник: Physical Review B
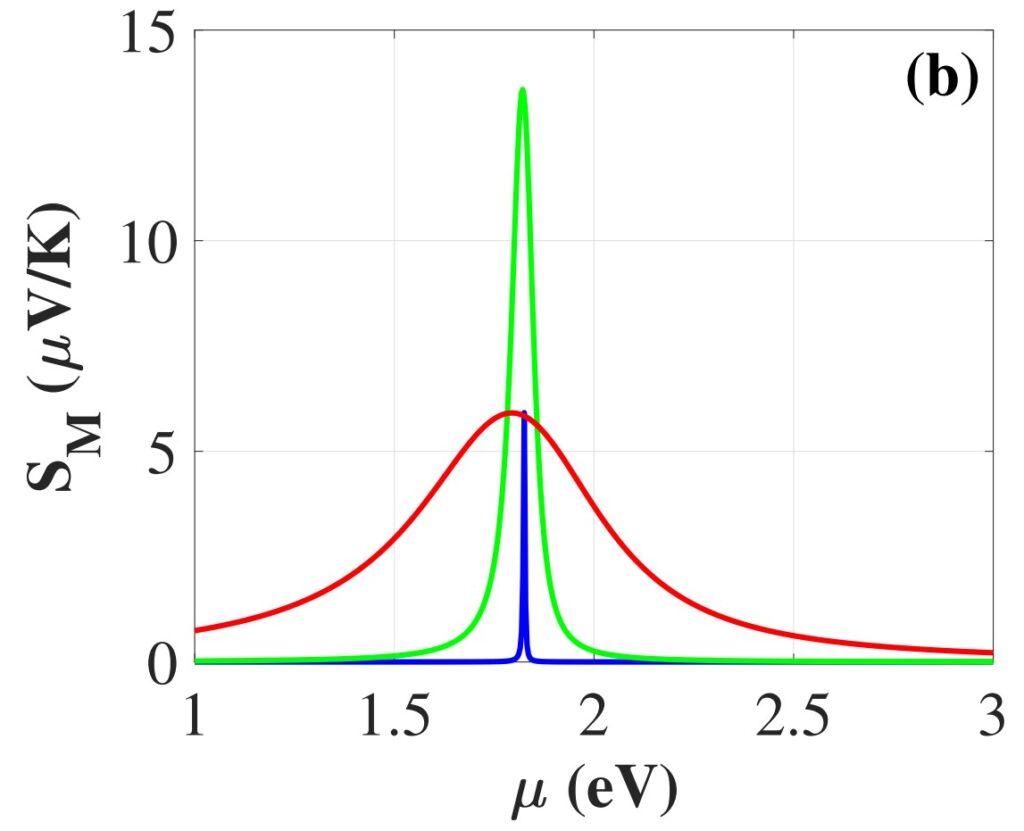
Рисунок 6. Зависимость коэффициента Зеебека от химического потенциала для параболического закона дисперсии при квантовом числе j = 1, вычисленная в теории Мотта, при разных значениях параметра размазывания: τ /ℏ=483.09 eV^(-1) соответствует синему графику, τ /ℏ=38.65 eV^(-1) — зеленому графику и τ /ℏ=3.86 eV^(-1) — красному графику. Источник: Physical Review B
Однако оказалось, что даже в случае сильного размытия подходы Кельвина и Мотта дают качественно разные результаты, особенно в том, что касается изменения знака коэффициента Зеебека. Последнее важно, так как это изменение знака описывает важный физический эффект — топологический фазовый переход.
«Формуле Кельвина более ста пятидесяти лет, Формуле Мотта — почти семьдесят. Удивительно, что карбоновые нанотрубки позволяют выявить разницу между двумя столь почтенными теориями, — объясняет Алексей Кавокин, директор Международного центра теоретической физики имени А. А. Абрикосова МФТИ. — Все дело в режиме баллистического транспорта, который был лишь теоретической абстракцией во времена Кельвина и Мотта, но стал экспериментальной реальностью в наши дни».
Полученные теоретические результаты, в особенности с дальнейшими экспериментальными исследованиями, которые предстоит провести, могут быть использованы для создания эффективных источников энергии для разнообразных микро- и наномеханических устройств, для которых традиционные литий-ионные технологии могут оказаться не настолько полезными.

