Ученые из МФТИ, ОИВТ РАН и ВШЭ методом молекулярной динамики смоделировали свойства системы метан–этан. Численное решение моделей было выполнено на суперкомпьютерах при условиях, экономически выгодных для переработки природного газа. Результаты исследований опубликованы в Russian Journal of Physical Chemistry A.
Природный газ — ценнейший энергоресурс и сырьевой компонент для получения органических соединений. Состав природного газа определяется его месторождением. Основная доля, от 70 до 99 %, принадлежит метану, остальное приходится на этан и пропан. Кроме углеводородов, в природном газе в небольших количествах могут содержаться и неорганические вещества: сероводород, азот, углекислый газ и другие.
Разделение на составляющие смеси, которую представляет собой природный газ, осуществляют разными методами. Наиболее широкое применение получило глубокое охлаждение. При его проведении для сжижения газов опускают температуру до минус 100 °C и ниже либо повышают давление. Превращаются из газа в жидкость в первую очередь вещества, у которых выше температура кипения. Вследствие этого их содержание в жидкой фазе становится в несколько раз больше, чем в паровой. Путем подбора условий глубокого охлаждения можно получить жидкость заданного состава, но есть ограничение: переработка природного газа в промышленных масштабах экономически выгодна в диапазоне давления от 34 до 39 атм и температуры от – 35 до – 45 °C.
Условия разделения газов, оптимальные с экономической и технической точки зрения, зависят от их состава и используемого оборудования. Определяют оптимальные условия, как правило, в ходе лабораторных экспериментов, что дорого и трудозатратно. Инновационное решение данной проблемы — разработка математических и компьютерных моделей процесса, имеющих высокую прогностическую точность. Ученые из МФТИ, ОИВТ РАН и ВШЭ с помощью метода молекулярной динамики смоделировали парожидкостное равновесие и свойства межфазных границ в системе метан–этан при давлении от 4 до 60 атм и температуре от – 20 до – 70 °C. Для достижения точности моделей ученые включили в них множество параметров: соотношение молекул метана и этана в системе, плотности и вязкие напряжения жидкости и газа, и другие. В связи со сложностью и громоздкостью моделей их численное решение выполнялось на суперкомпьютерах. Суперкомпьютеры получили свое название благодаря улучшенным техническим характеристикам, в том числе большей производительности и скорости вычислений по сравнению с остальными современными компьютерами.
Следует пояснить, что метод молекулярной динамики предполагает изучение изменений во времени в системе метан–этан путем описания движения и взаимодействия молекул этих веществ уравнениями классической механики. При расчетах атом углерода и водорода в молекулах рассматривался учеными как единое целое, так называемый псевдоатом. Для моделирования изотермических условий, иными словами, постоянства температуры в системе, был учтен тепловой резервуар и потери на трение. Такой метод вычислений называют термостатом Нозе—Гувера. Моделирование постоянного давления осуществлялось методом вычислений, именуемым баростатом Шиноды. При реализации этого метода меняются размеры вычислительной ячейки таким образом, чтобы давление на ее стенки соответствовало нужному. Численное решение уравнений Ньютона проводилось до тех пор, пока изучаемая система не станет равновесной, то есть плотность жидкости и газа прекратит изменяться с течением времени.
«Мы обнаружили, что в системе метан–этан граница раздела жидкой и газовой фазы самопроизвольно обогащается метаном, — говорит Дмитрий Ленев, ассистент кафедры физики высокотемпературных процессов Физтех-школы электроники, фотоники и молекулярной физики МФТИ. — Нами получена формула, позволяющая по опытным данным вычислить величину адсорбции в поверхностном слое двухкомпонентной системы, не используя при этом молекулярно-кинетическую теорию идеального газа».
Идеальный газ — это тоже модель, имеющая свои допущения, которые вносят ошибки в результаты расчетов. Тем не менее химические вычисления традиционно выполняют при этих допущениях. Однако результаты такого моделирования при высоких концентрациях метана существенно расходятся с опытными данными. Достижение авторов — в выводе формулы без допущений молекулярно-кинетической теории, что дает возможность получения в ходе расчетов более точных значений величины адсорбции даже при большом количестве метана в системе.
Для проверки разработанных моделей ученые выполнили два варианта расчетов адсорбции, то есть количества вещества, сконцентрированного на единице площади поверхностного слоя. Кривая, построенная при решении фундаментального уравнения адсорбции Гиббса, в данном случае использовалось для сравнения. Надо подчеркнуть, что согласуются результаты обоих вычислений величины адсорбции метана в зависимости от его доли в жидкой фазе при минус 60 °C (Рисунок 1). Это доказывает выполнение поставленных при моделировании задач. Температура минус 60 °C была выбрана для ускорения расчетов и снижения их погрешности. При более высоких температурах этан близок к сверхкритическому состоянию, при котором исчезают различия между газовой и жидкой фазой.
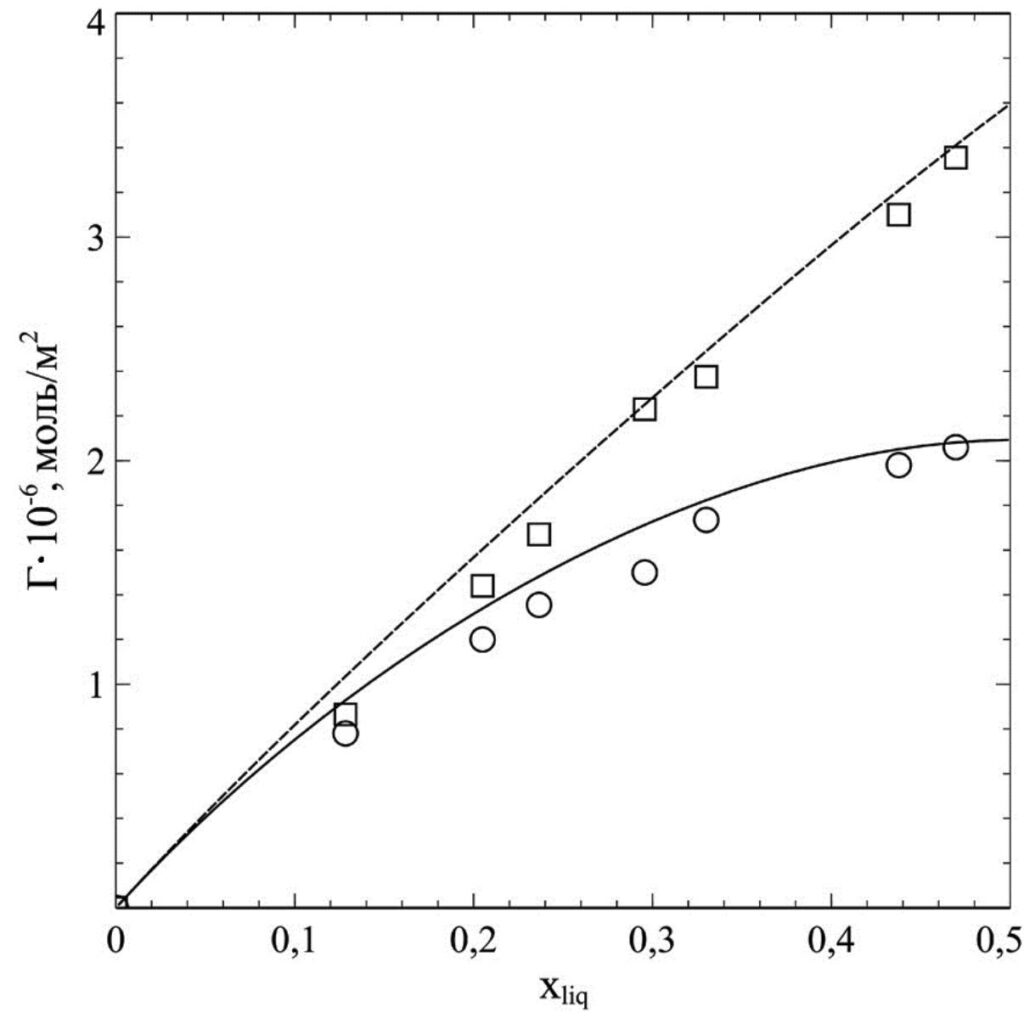
Рисунок 1. Зависимость адсорбции метана Г (моль/м2) на границе раздела фаз метан–этан от доли метана в жидкости Xliq при минус 60 °C. Сплошная линия (круги) — изотерма адсорбции Гиббса, пунктирная (квадраты) — смоделирована методом молекулярной динамики. Источник: Russian Journal of Physical Chemistry A.
Известно, что с ростом величины адсорбции снижается коэффициент поверхностного натяжения, равный отношению поверхностной энергии к площади поверхности жидкости. Это наблюдается до момента предельного заполнения границы раздела фаз молекулами вещества, уменьшающими поверхностную энергию. Ученые установили, что в изучаемой системе поверхностное натяжение падает не только с ростом адсорбции, но и давления (Рисунок 2). Проверка качества моделирования в этом случае осуществлялась путем сопоставления расчетных и опытных данных. Важно, что результаты совпали, значит, модель верно построена.
«Получена линейная зависимость поверхностного натяжения от давления, — поясняет Дмитрий Ленев. — Она объясняется уменьшением разности плотностей и увеличением толщины границы раздела фаз».
Чем меньше поверхностное натяжение, тем выше растекание углеводородов. Это, в свою очередь, определяет образование водонефтяных и газонефтяных эмульсий — крайне нежелательного явления при газо- и нефтепереработке.
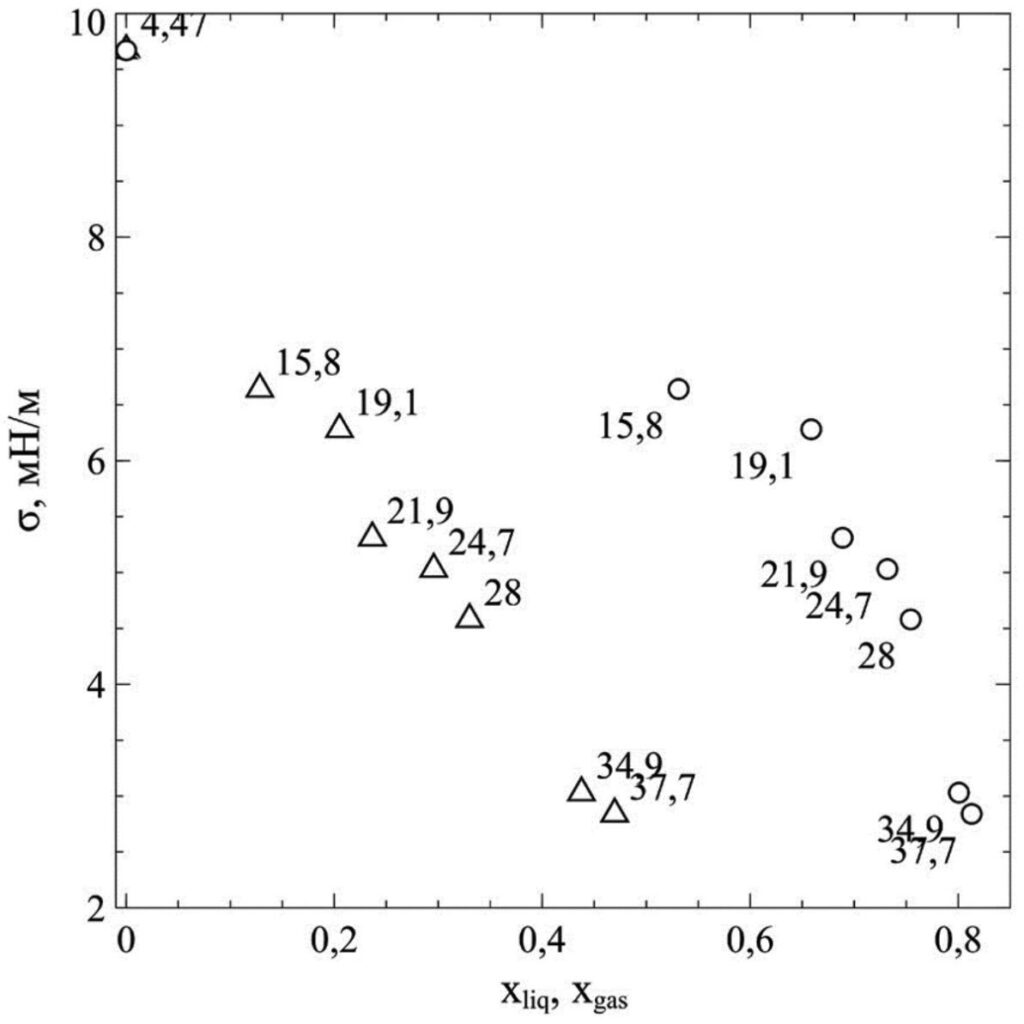
Рисунок 2. Зависимость поверхностного натяжения σ (мН/м) смеси метана и этана от доли метана в жидкой (треугольники) Xliq и газовой (круги) Xgas фазе при минус 60 °C. Цифрами показано давление соответствующей точки (атм). Источник: Russian Journal of Physical Chemistry A.
Построенные учеными математические и компьютерные модели, а также полученные численные решения найдут применение при проведении работ по разделению газовых смесей, в частности, природного газа, методом глубокого охлаждения.

