Международный коллектив ученых из России и Китая представил исследование, посвященное W-представлениям для многосимвольных статистических сумм и их β-деформаций. Работа опубликована в журнале Physics Letters B и содержит важные результаты, расширяющие наше понимание обобщений известных моделей математической физики, таких как гипергеометрические функции Гурвица.
В последние годы наблюдается значительный прогресс в понимании связи между W-представлениями для тау-функций и суперинтегрируемостью матричных моделей. Эти исследования открывают новые горизонты в теоретической физике, особенно в области матричных моделей и их приложений в статистической механике и теории поля. Однако, несмотря на достигнутые успехи, многие темы, такие как многокомпонентные распределения, статистические суммы и их интегральные представления, оставались недостаточно изученными.
Тау-функции — это специальные функции, которые играют ключевую роль в теории интегрируемых систем и в статистической механике. Для описания таких систем, как квантовые поля или статистические модели твердого тела, используются матричные модели. W-представления позволяют описывать классы тау-функций и их связи с матричными моделями, предоставляя удобный инструмент как для аналитического исследования таких моделей, так и для численного моделирования.
Целью недавнего исследования было обобщение W-представлений для многосимвольных статистических сумм. Ученые обобщили уже известные модели и построили интегральные представления для таких сумм, что может привести к новым открытиям в области матричных моделей и их приложений.
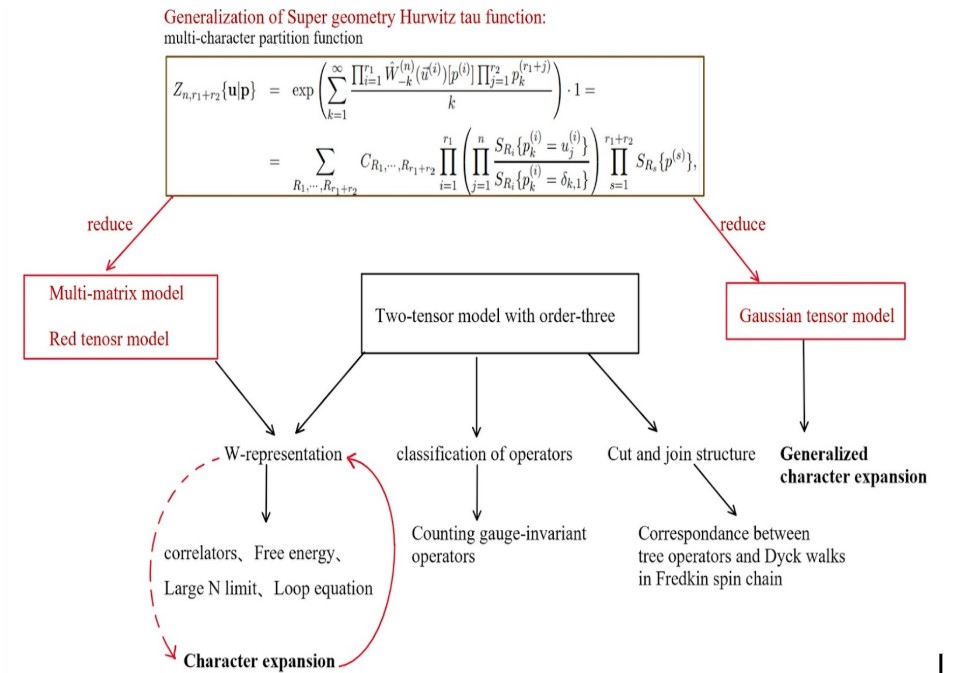
Рисунок 1. Обобщение гипергеометрической тау-функции Гурвица и его связь с прикладными моделями и методами. Источник: авторский контент Lu-Yao Wang.
Исследование включало в себя несколько ключевых этапов. Во-первых, были построены обобщения W-представлений на произвольное количество временных переменных, что позволяет более гибко подходить к описанию физических систем-. Во-вторых, были предложены интегральные представления для статсумм, которые описываются тензорными и многоматричными моделями с многоследовыми взаимодействиями. В-третьих, была исследована β-деформация W-представлений.
«Наше исследование подчеркивает важность W-представлений и их обобщений для понимания сложных физических систем. Мы надеемся, что наши результаты станут основой для будущих исследований в этой области. В дальнейшем необходимо изучить связь W-представлений с другими математическими структурами, такими как алгебры Ли и группы симметрий», — рассказал Александр Пополитов, научный сотрудник лаборатории математической и теоретической физики МФТИ.
Обобщения W-представлений позволяют более глубоко понять связи между различными физическими моделями и расширить существующие теории.
Они могут быть применены в разработке новых моделей для описания квантовых систем и статистической механики, для решения задач квантовых вычислений, углубления нашего понимания фазовых переходов и критических явлений.
1

