Ученые из Московского политехнического университета и МФТИ представили теоретическую работу, посвященную введению дополнительных соотношений неопределенности Гейзенберга в (1+3)-мерном пространстве Минковского и в (1+4)-мерной расширенной модели пространства. Это исследование может изменить наши представления о времени, пространстве и материи. Работа опубликована в RENSIT: Radioelectronics. Nanosystems. Information Technologies.
Идея о взаимосвязи пространства и времени восходит к работам Германа Минковского, который в 1908 году предложил концепцию пространственно-временного континуума.
«Никто никогда не наблюдал, — сказал Минковский. — никакого места, кроме как в какой-то момент времени, и никакого времени, кроме как в каком-то месте». Минковский называет точку в пространстве, соответствующую данному моменту времени, «мировой точкой», а совокупность всех мировых точек кратко — «миром». Таким образом, любое тело, существующее в течение некоторого времени в пространстве, будет соответствовать определенной кривой — мировой линии.
«…Весь мир, кажется, распадается на такие мировые линии, — продолжает Минковский свою речь.— физические законы могли бы найти свое наиболее совершенное выражение, как соотношение между этими мировыми линиями».
Его работа положила начало теории относительности, в которой пространство и время рассматриваются как единое целое. В дальнейшем Вернер Гейзенберг сформулировал принцип неопределенности, который стал краеугольным камнем квантовой механики. Однако до сих пор оставались вопросы о том, как расширить эти концепции в более высокие размерности и как они соотносятся с другими физическими величинами, такими как масса и интервал.
Принцип неопределенности Гейзенберга — это фундаментальный принцип квантовой механики, который утверждает, что невозможно одновременно точно определить пару связанных переменных, таких как положение и импульс частицы.
В своей недавней работе российские ученые предложили ввести дополнительные соотношения неопределенности, связывающие массу и интервал в расширенной модели пространства. Это 5-мерная модель расширенного пространства (МРП), в которой к трем пространственным координатам и времени добавлен интервал как 5 координата. В этой модели соотношение между энергией, импульсом и массой оказывается частным случаем теоремы Пифагора в 5-мерном пространстве, сопряженном с координатным пространством.
Представленная в работе (1+4)D модель расширенного пространства основывается на физической гипотезе, состоящая в том, что масса (масса покоя) и сопряженная ей величина – действие (интервал) являются динамическими переменными. Величины этих переменных определяются взаимодействием полей и частиц. Модель расширенного пространства является непосредственным обобщением Специальной теории относительности (СТО).
В СТО интервал и масса покоя частиц являются инвариантами, а в МРП они могут меняться. На основе сделанных предположений в МРП построены расширенные уравнения Максвелла, которые наряду с электромагнитным взаимодействием описывают также и гравитационные эффекты, а также имеют структуру, похожую на релятивистское обобщение уравнения Шредингера в свободном от поля пространстве в форме уравнения Клейна-Гордона.
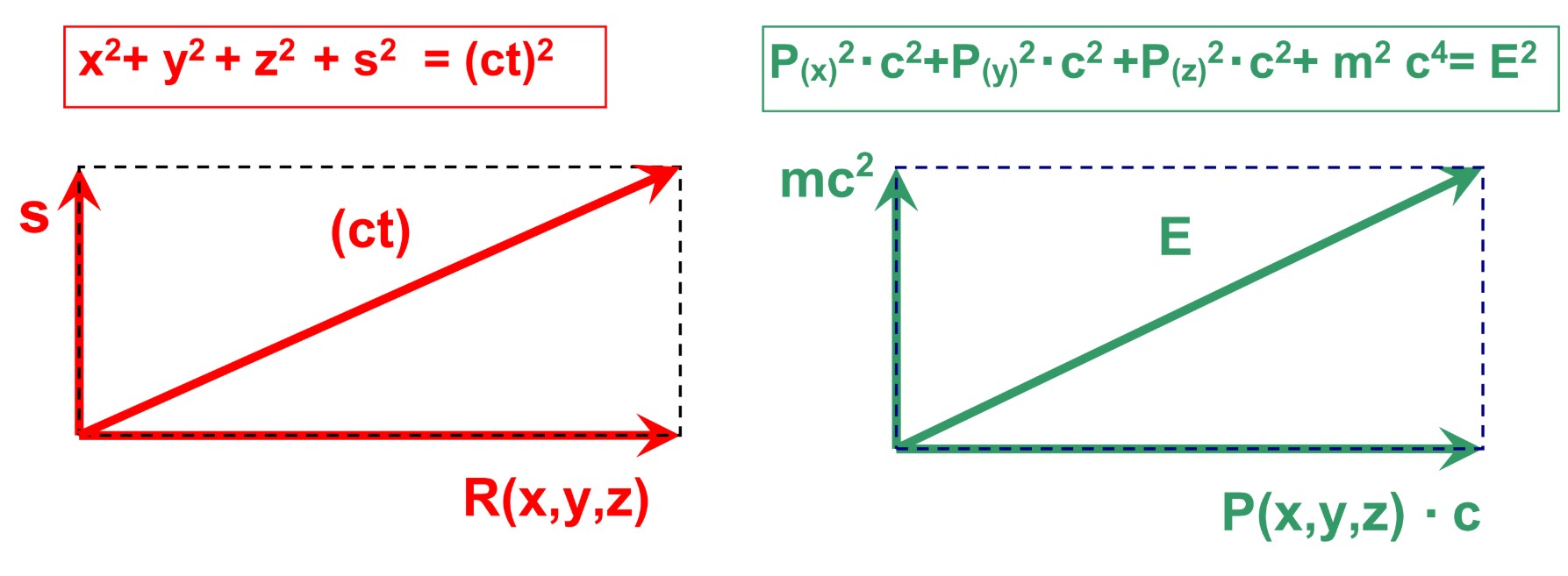
Рисунок 1. Теорема Пифагора в пятимерной расширенной (1+4)D модели. Оси абсцисс соответствуют трехмерному координатному пространству (красный) и трехмерному пространству импульсов (зеленый).
«Наше исследование подчеркивает важность дополнительных измерений в физике и показывает, что традиционные представления о массе и интервале могут быть значительно расширены. Мы надеемся, что это приведет к новым открытиям в области квантовой механики и теории поля», — рассказал Евгений Седельников, доцент кафедры общей физики МФТИ.
Новизна исследования заключается в том, что принцип неопределенности расширяется на вводимые в модели дополнительные координаты — интервал и массу, которые до сих пор рассматривались как инвариантные величины.
«Модель расширенного (1+4)D пространства была создана уже более 25 лет назад, — вспоминает доцент кафедры общей физики МФТИ Дмитрий Ципенюк. — В свое время, после выхода очередной нашей статьи, посвященной развитию различной аспектов нашей модели, я три раза ходил к академику В. Л. Гинзбургу и рассказывал ему наши работы — два раза до присуждения В. Л. Гинзбургу Нобелевской премии и один раз после. Виталий Лазаревич каждый раз внимательно, около часа выслушивал меня и каждый раз старался помочь — отводил к своим коллегам или сотрудникам для более детального изучения наших статей. Однажды, встретив меня на своем знаменитом семинаре в ФИАНЕ, Виталий Лазаревич одобрительно похлопал по плечу и сказал “а пятимерное пространство, давай”».
Если новый подход окажется правильным, то это приведет к большей геометризации физики, чем та, которая была достигнута в теории относительности Эйнштейна. Всю физику в расширенной модели пространства можно понимать как прикладную геометрию.

